ICO and GreyCTF Finals 2025
introduction#
Over the last week of June, I participated in both the inaugural International Cybersecurity Olympiad and GreyCTF Finals. It was quite a fun experience (I spent an entire week at NUS), and I thought I’d share my experience, along with some writeups for the more interesting challenges.
ICO#
The International Cybersecurity Olympiad was a seven1 day event, hosted by the NUS School of Computing. While the event wasn’t perfect2 I still rather enjoyed it overall. All eight Singaporean participants received medals for the event, with me receiving a gold.
The competition was split over two days; challenges were split between “attack style” and “defence style” (red and blue), with 9 hours of competing overall. While I don’t exactly understand how the challenges were split3, there was still a healthy mix of categories, along with a dose of challenges contributed by NUS GreyHats. ICO was also the first CTF where I actually attempted (but didn’t solve) some non-ret2win pwn challenges.
Day 1 - ICO Red#
I solved four challenges and obtained 350 points. Unfortunately, I was one challenge away from FCing crypto, but that challenge had 0 solves total (I think). Most of the challenges were also solvable with ChatGPT. I will be writing about three challenges: Crypto - Funny Little Trial, Pwn - Carpark, and Rev - Complicated. Out of these three, I only managed to solve the crypto during the competition itself (and spent over half my time trying the rev); the pwn and the rev are upsolved.
Crypto - Funny Little Trial#
from Crypto.Util.number import getStrongPrime, bytes_to_long
import json
NBITS = 2048
e = 65537
p, q = getStrongPrime(NBITS, e = e), getStrongPrime(NBITS, e = e)
if p < q:
p, q = q, p # Ensure p is always greater than or equal to q
n = p * q
s = (pow(p, q, n) + pow(q, p, n)) % n
with open("../flag.txt", "rb") as f:
flag = f.read().strip()
with open("chall.json", "w") as f:
json.dump({
"n": n,
"e": e,
"c": pow(bytes_to_long(flag), e, n),
"s": s
}, f)
A normal RSA setup, except we are also given the value of \(\left(p^q + q^p\right) \bmod n\). Taking modulo \(p\), we can see that
\[ \begin{align} p^q + q^p &\equiv q^p\\ &\equiv q \pmod p \end{align} \]where the last line is given by Fermat’s Little Theorem.4 Similarly, \(p^q + q^p \equiv p \pmod q\), so by CRT \(p^q + q^p \equiv p + q \pmod n\). Since \(p + q < n\), the value given is equal to \(p + q\) directly. Now, we can simply solve a quadratic to get the values of \(p\) and \(q\) and recover the flag.
Flag: ICO{f3rMaT5_l1L_ThM_i5_Tr1Vi4L_r1t3???}
Pwn - Carpark#
Show challenge source
// g++ -g -no-pie chall.cpp -o chall
#include <stdio.h>
#include <vector>
using namespace std;
using ll = long long;
#define CARPARK1_SPACE 10
#define CARPARK2_SPACE 20
void setup(){
setvbuf(stdout, NULL, _IONBF, 0);
setbuf(stdin, NULL);
setbuf(stderr, NULL);
}
struct Carparks {
ll carpark1[CARPARK1_SPACE];
vector<ll> carpark2 = vector<ll>(CARPARK2_SPACE, 0);
};
int main() {
setup();
Carparks cp;
ll* carpark1 = cp.carpark1;
vector<ll>& carpark2 = cp.carpark2;
for (int i = 0; i < CARPARK1_SPACE; i++) {
carpark1[i] = 0;
}
int choice;
while (true) {
puts("1. Change carpark1 car");
puts("2. View carpark1 car");
puts("3. Change carpark2 car");
puts("4. View carpark2 car");
printf("> ");
scanf("%d", &choice);
if (choice < 1 || choice > 4) {
puts("Invalid option!");
continue;
}
int slot;
puts("Which car?");
printf("> ");
scanf("%d", &slot);
if (choice == 1) {
if (slot < 0 || slot > CARPARK1_SPACE) {
puts("Invalid slot!");
continue;
}
ll newval;
printf("New value > ");
scanf("%lld", &newval);
carpark1[slot] = newval;
} else if (choice == 2) {
if (slot < 0 || slot > CARPARK1_SPACE) {
puts("Invalid slot!");
continue;
}
printf("Value of car %d is %lld\n", slot, carpark1[slot]);
} else if (choice == 3) {
if (slot < 0 || slot > CARPARK2_SPACE) {
puts("Invalid slot!");
continue;
}
ll newval;
printf("New value > ");
scanf("%lld", &newval);
carpark2[slot] = newval;
} else {
if (slot < 0 || slot > CARPARK2_SPACE) {
puts("Invalid slot!");
continue;
}
printf("Value of car %d is %lld\n", slot, carpark2[slot]);
}
}
}
The important part is the bounds check:
if (slot < 0 || slot > CARPARK1_SPACE) {
puts("Invalid slot!");
continue;
}
There is an off-by-one error here; the correct maximum value check should be slot >= CARPARK1_SPACE. This allows us to overwrite the value right after the 10th element in carpark1, which happens to be the pointer to carpark2. As we can also read and write from carpark2, we essentially have an arbitrary read and write. We can then simply read an address from GOT to obtain the libc offset, then write the address of a one_gadget at the GOT entry of a function like puts or scanf. Our gadget will then be ran when the corresponding function is called, granting us access to a shell.
Flag: ICO{h0W_m4nY_C4R5_w0UlD_4_c4rpArK_p4rK_1F_a_carp4rK_c0u1d_p4rk_car5}
Rev - Complicated#
~ $ ./complicated
meowmeow
not nice
The binary appears to be a classic password checker. Decompiling the binary, we get
__int64 __fastcall main(int a1, char **a2, char **a3)
{
char *v4; // [rsp+8h] [rbp-8h]
__isoc99_scanf(&unk_41004, &s, a3);
v4 = strchr(&s, 10);
if ( v4 )
*v4 = 0;
if ( strlen(&s) == 80 && (unsigned int)sub_36DF1() )
puts("nice");
else
puts("not nice");
return 0LL;
}
_BOOL8 sub_36DF1()
{
return (unsigned int)sub_1DC07((unsigned int)byte_8006F) == 1040;
}
__int64 __fastcall sub_1DC07(int a1)
{
return sub_3CE41((unsigned int)(byte_80067 + a1));
}
__int64 __fastcall sub_3CE41(int a1)
{
return sub_3F9A0((unsigned int)(a1 - byte_8005C));
}
__int64 __fastcall sub_3F9A0(int a1)
{
return sub_27A86((unsigned int)(a1 - byte_80043));
}
__int64 __fastcall sub_27A86(int a1)
{
return sub_CFDE((unsigned int)(byte_8006E + a1));
}
__int64 __fastcall sub_CFDE(int a1)
{
return sub_3BFBC((unsigned int)(a1 - byte_80046));
}
__int64 __fastcall sub_3BFBC(int a1)
{
return (a1 == 92) + (unsigned int)sub_3B722((unsigned int)byte_80077);
}
...
It can be seen that the input must be 80 characters long, and must then satisfy a lot of arithmetic expressions involving each character. At first, I tried to use angr to solve it, but it ended up not working, making me waste 2 hours trying.5 About 1 hour before the end of the competition, I started trying to write my own “disassembler” to automatically extract the arithmetic operations from the ELF file, then use z3 to symbolically solve for each character, but I didn’t manage to finish in time :( In hindsight I probably should have disassembled with objdump or something and worked on that instead of the raw bytes, or asked ChatGPT to write a parser for me. Oh well.
Here is the author’s solve script:
# coding: utf-8
from unicorn import *
import base64
from unicorn.x86_const import *
from capstone import *
import z3
cs = Cs(CS_ARCH_X86, CS_MODE_64)
cs.detail = True # Enable detailed instruction information
with open("./complicated", "rb") as f:
chal = f.read()
mu = Uc(UC_ARCH_X86, UC_MODE_64)
mu.mem_map(0x1337000, 0x100000)
mu.mem_map(0x7ffff000000, 0x100000)
mu.mem_write(0x1337000, chal)
mu.reg_write(UC_X86_REG_RBP, 0x7ffff050000)
mu.reg_write(UC_X86_REG_RSP, 0x7ffff050000)
eqn = []
eqns = []
# Define a hook_code function to print disassembled instructions
def hook_code(uc, address, size, user_data):
global eqn
global eqns
# Read the instruction bytes from emulated memory
code_bytes = uc.mem_read(address, size)
for i in cs.disasm(code_bytes, address):
if i.mnemonic == 'movzx' and "eax, byte ptr [" in i.op_str:
val = int(i.op_str.split(' + ')[1][:-1], 16) + i.address + 7
offs = val - 0x80040 - 0x1337000
eqn.append(f'flag[{offs}]')
elif "cmp" == i.mnemonic:
val = i.op_str.split(', ')[1]
eqn.append(val)
body = eqn[1:-1]
body = str(eqn[0])+''.join([''.join(str(j) for j in body[i:i+2][::-1]) for i in range(0, len(body), 2)])+'=='+eqn[-1]
eqns.append(body)
eqn = []
elif "sub" == i.mnemonic and 'eax, edx' == i.op_str:
eqn.append("-")
elif "add" == i.mnemonic and 'eax, edx' == i.op_str:
eqn.append("+")
mu.hook_add(UC_HOOK_CODE, hook_code)
mu.emu_start(0x1337000+0x36df1 , 0x1337000+0x3d60a)
s = z3.Solver()
flag = [z3.BitVec(f"flag_{i}", 8) for i in range(80)]
for eqn in eqns:
s.add(eval(eqn))
print(s.check())
m = s.model()
f = ''
for i in flag:
f += chr(int(m[i].as_long()))
print(base64.b64decode(f))
It was about the same idea as mine, but instead of statically analysing the ELF/disassembly, the binary was emulated to extract the checks. After that, z3 is used to find the characters of the input, which is then base 64 decoded to retrieve the flag.
Flag: ICO{callcallcallcallcallcallcallcallcallcallcallangrcallme}
Day 2 - ICO Blue#
For some reason, the organisers decided to change the score distribution the night before the competition. Day 1 had 700 points over 8 challenges, with a welcome challenge at 50 points and most other challenges at 100 points. Day 2 had 21(!!) challenges, with not just one but two welcome challenges worth 10 points each. The point distribution was also now more spread out, with most challenges having scores between 20 and 70 points. However, a lot of points were concentrated in the digital forensics category, which had 465 points across 13 challenges (although they were all part of one “big” challenge and had to be solved in order); a lot of people I talked to after the competition were not very happy with this arrangement.
I solved 19 challenges, earning 833 points. The challenges weren’t really that interesting to talk about; most of the challenges were trivial and could be ChatGPTed (with the exception of the CSIT-set pwn, which no one solved), so I’ll just be giving a brief overview of the entire digital forensics category.
Digital Forensics#
The challenges were split into three phases: Vunerability Assessment, Forensics, and AP (I don’t know what it stands for). For phase 1, we were first given an IP, and asked to scan it to find any interesting services running. Then, we were asked to determine the OS that was running on the target machine. Both of these can be done relatively easily with nmap.
Next, we were asked to access the vulnerable service (it was HTTP). Doing so brought up a to-do list, mentioning the vulnerability CVE-2024-4577. We then had to use metasploit to exploit the website to gain shell access on the remote machine, and were tasked to retrieve a packet capture file from the desktop, concluding phase 1.
In phase 2, we had to analyse the obtained packet capture, dig through it to find evidence of file transfer between a malicious attacker and the machine, and recover the malware file that was transferred from the attacker. Then, we had to analyse the malware in phase 3, and answer some relatively simple questions about its functions.
Miscellaneous Thoughts#
ICO didn’t really go as smoothly as I had hoped it would. We had no team Singapore group chat until day 1 of ICO, and our only method of communication with the organisers was through email, so we had basically no way to contact other members of team Singapore unless we already knew them beforehand. We also had no team leader and no volunteer, so we often didn’t receive important information that all the other teams received (I think).
Aside from communication issues, there were also many problems on the technical side of things. A few days before ICO even started, we received a password-encrypted zip file meant to include challenge files for ICO Blue, the second day of the competition. Unfortunately, the zip file could be cracked with bkcrack, resulting in a leak of the challenge files. While this was raised up to the organisers, no action was taken.
The day before ICO Red, we were given a technical briefing, in which it was claimed that the challenge files sent were actually meant for ICO Red. This was confusing, especially because the zip file itself was named ICOBlue.zip. We tried to seek clarification, but no clear explanation was ever given. At around 7pm that day, an email was sent out containing ICOBlue.zip again, but this time with the password included.
Just 8.5 hours before ICO Red was supposed to start, I was informed that the zip file would not be used.
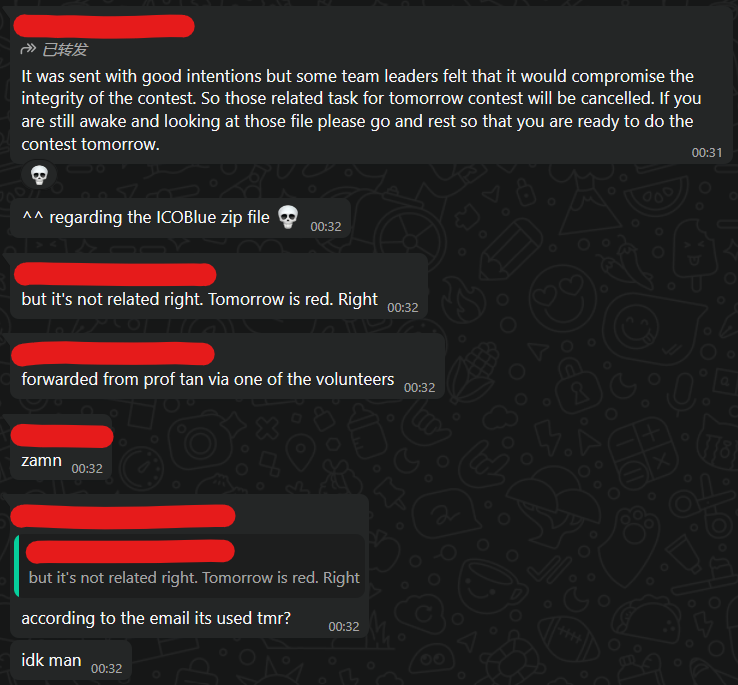
Apparently, the message was disseminated amongst the volunteers chat. As mentioned before, team Singapore had no team leader of volunteer, so we were not immediately made aware of this change, and it took a fellow participant to forward the message from another volunteer who sent it to them. The organisers, being present in the team Singapore group chat, read the messages but did not reply with a clarification.
About an hour before ICO Red started, I was told by a volunteer that the contest duration would be shortened from the original 5 hours to 3 hours, owing to some challenges being removed. This was not announced in the team Singapore group chat; the only time it was officially announced to team Singapore was in the briefing right before the competition. However, about 2.5 hours into the competition, it was announced that the duration would be extended by another hour, to 4 hours in total.
The night before ICO Blue, the second day of the competition, we were sent credentials to connect to a jump server and Kali VM that was required to be used for some challenges. Somewhat expectedly, there were many technical issues that arised, culminating in a 55 minute delay of the start of the competition. During the closing ceremony, this was explained to be because of safety precautions being automatically triggered within the NUS servers.
I am somewhat disappointed and sad that the inaugural ICO was not very well organised; however, given that majority of the Olympiad was organised by one person(?) in just six months, it is not very unexpected. With a proper organising committee and scientific committee set up, I hope that ICO 2026 will surely go much more smoothly.
GreyCTF finals#
GreyCTF finals were held overnight across two days in NUS COM1. My team didn’t do so well for this; I think we all collectively gave up around 11pm and started fooling around.6 It also didn’t help that I stayed up until 2:30am playing mahjong the previous night.
I’ll be writing about all except one of the cryptos, althogh I only managed to solve three of them during the competition. As always, the challenges were pretty high-quality and nice to solve (…maybe except for meow log meow log e)
Safe XOR#
def safeXor(a,b): # in case of none input
if a is None: return b
if b is None: return a
if a==b: return not a
return None
from functools import reduce
flag = b"grey{?????????????????????}"
iv = [True if int(i) else False for i in bin(int(flag.hex(),16)).lstrip("0b")]
for _ in range(2**999):
iv = iv[1:] + [reduce(safeXor,iv)]
assert iv == [...]
An important observation to make is that the safeXor function is the same as addition mod 3, with None as 0, False as 1, and True as 2. We can construct the matrix representing the LFSR in sage under GF(3), then invert, exponentiate, and finally multiply with the final state to recover the original state and get the flag.
from Crypto.Util.number import long_to_bytes
final = [...]
l = len(final)
M = matrix(GF(3), l)
for i in range(l-1):
M[i, i+1] = 1
M[-1] = 1
Minv = M.inverse()
final = vector(map(GF(3), [0 if x is None else x+1 for x in final]))
flag = Minv^(2^999)*final
flag = int("0"+"".join(str(int(x)-1) for x in flag), 2)
print(long_to_bytes(flag))
Flag: grey{!safe,_!xor,_wow..,..,.,}
DLog24#
p = 4159930969
f = x^24 + 11*x^23 + 17*x^22 + 4159930747*x^21 + 4159930096*x^20 + 974*x^19 + 9643*x^18 + 6555*x^17 + 4159887259*x^16 + 4159860403*x^15 + 78895*x^14 + 233115*x^13 + 4159929335*x^12 + 4159584268*x^11 + 4159760950*x^10 + 223085*x^9 + 195174*x^8 + 4159894366*x^7 + 4159855742*x^6 + 4159919343*x^5 + 8317*x^4 + 2638*x^3 + 45*x^2 + 4159930938*x + 1
R = Zmod(p^24)[x].quo(f)
flag = int.from_bytes(b"grey{?????????????????????}")
c = R(x)^flag
assert c == R(...)
A standard DLP challenge in \(\mathbb{Z}/p^{24}\mathbb{Z}/f\), where \(f\) is an irreducible polynomial of degree 24. I spent a grand total of around 12 hours on this challenge, trying to Pohlig-Hellman it because the order was “smooth enough”. Spoiler alert: it didn’t work. Then after about 11 hours of going back and forth between ChatGPT and VSCode I decided to be smart and gave up.
You can solve the DLP by first solving over mod \(p\), then lifting your way through \(p^2, p^3, \dots\) all the way until \(p^{24}\) through Hensel lifting, but Sage can also oneshot it with p-adics pretty easily.
My solve:
p = 4159930969
K.<x> = Zmod(p^24)[]
f = x^24 + 11*x^23 + 17*x^22 + 4159930747*x^21 + 4159930096*x^20 + 974*x^19 + 9643*x^18 + 6555*x^17 + 4159887259*x^16 + 4159860403*x^15 + 78895*x^14 + 233115*x^13 + 4159929335*x^12 + 4159584268*x^11 + 4159760950*x^10 + 223085*x^9 + 195174*x^7 + 4159894366*x^6 + 4159855742*x^5 + 4159919343*x^4 + 8317*x^4 + 2638*x^3 + 45*x^2 + 4159930938*x + 1
F.<x> = Zp(p, 24).ext(f)
h = ...
g = x
print(long_to_bytes(ZZ(h.log()/g.log())))
Flag: grey{h3h3heheh3h3_1_luv_p0lynom1als_s0_much_sie_ist_me1ne_best1e!1!11!!11!!1!!!11!!11!}
Meow Log Meow Log Meow E#
from Crypto.Util.number import bytes_to_long, getStrongPrime
from random import randint
import json
load("../secret.sage") # e_power
with open("../flag.txt", "rb") as f:
FLAG = f.read()[:-1]
BITS = 2048
e = 65537
p, q = getStrongPrime(BITS, e), getStrongPrime(BITS, e)
n = p * q
phi = (p - 1) * (q - 1)
d = inverse_mod(e, phi)
assert d > n ^ 0.292, "No Boneh-Durfee for you!"
zr = Zmod(n)
m1 = bytes_to_long(FLAG)
po = randint(65, 128)
# Hint: HUH? WHAT'S E DOING HERE,
# I THOUGHT THIS WAS A FINITE FIELD????!?!?!?!?!?!?!
m2 = e_power(m1, zr, po)
c1 = zr(m1) ^ e
c2 = zr(m2) ^ e
with open("chall.json", "w") as f:
json.dump({
"n": int(n),
"e": int(e),
"c1": int(c1),
"c2": int(c2),
"po": int(po),
}, f, indent=4)
print("Challenge generated and saved to chall.json")
I am not a fan of this challenge. A non-trivial part of the difficulty comes from the fact that e_power is not made known to players. It also doesn’t help that e also represents the public exponent in RSA, leading to further confusion. About 1.5 hours into the competition, the challenge was modified to include the hint that e_power(x, y, z) calculates e^x in y; the purpose of z was still not made clear.
When considering the exponential function on non-standard structures , the first thing one should think of should be the Maclaurin series expansion of \(e^x\):
\[ e^x = \sum_{k=0}^\infty \frac{1}{k!} x^k \]The third argument to e_power can then be interpreted as an indicator to how many terms should be taken from the expansion. I had originally thought that 77 would mean that the resulting polynomial would have degree 77, but it actually means that the polynomial would have 77 terms (so degree 76).
From there, we can construct two polynomials with the flag as a common root:
\[ \begin{align} f(x) &= m^{65537} - c_1\\ g(x) &= (E(x))^{65537} - c_2 \end{align} \]We can then take their GCD (using half-GCD, since normal GCD would be too slow) to get the flag. A point to note is that exponentiating the Maclaurin expansion normally would take too much memory and crash Sage; the fix is to specify the other polynomial as a modulus when exponentiating.
from Crypto.Util.number import long_to_bytes
n = ...
c1 = ...
c2 = ...
e_power = Zmod(n)[x](taylor(e^x, x, 0, 76))
# halfgcd taken from https://github.com/jvdsn/crypto-attacks/blob/master/shared/polynomial.py
def _polynomial_hgcd(ring, a0, a1):
assert a1.degree() < a0.degree()
if a1.degree() <= a0.degree() / 2:
return 1, 0, 0, 1
m = a0.degree() // 2
b0 = ring(a0.list()[m:])
b1 = ring(a1.list()[m:])
R00, R01, R10, R11 = _polynomial_hgcd(ring, b0, b1)
d = R00 * a0 + R01 * a1
e = R10 * a0 + R11 * a1
if e.degree() < m:
return R00, R01, R10, R11
q, f = d.quo_rem(e)
g0 = ring(e.list()[m // 2:])
g1 = ring(f.list()[m // 2:])
S00, S01, S10, S11 = _polynomial_hgcd(ring, g0, g1)
return S01 * R00 + (S00 - q * S01) * R10, S01 * R01 + (S00 - q * S01) * R11, S11 * R00 + (S10 - q * S11) * R10, S11 * R01 + (S10 - q * S11) * R11
def fast_polynomial_gcd(a0, a1):
"""
Uses a divide-and-conquer algorithm (HGCD) to compute the polynomial gcd.
More information: Aho A. et al., "The Design and Analysis of Computer Algorithms" (Section 8.9)
:param a0: the first polynomial
:param a1: the second polynomial
:return: the polynomial gcd
"""
# TODO: implement extended variant of half GCD?
assert a0.parent() == a1.parent()
if a0.degree() == a1.degree():
if a1 == 0:
return a0
a0, a1 = a1, a0 % a1
elif a0.degree() < a1.degree():
a0, a1 = a1, a0
assert a0.degree() > a1.degree()
ring = a0.parent()
# Optimize recursive tail call.
while True:
print(f"[*] current degree: {a0.degree()}")
_, r = a0.quo_rem(a1)
if r == 0:
return a1.monic()
R00, R01, R10, R11 = _polynomial_hgcd(ring, a0, a1)
b0 = R00 * a0 + R01 * a1
b1 = R10 * a0 + R11 * a1
if b1 == 0:
return b0.monic()
_, r = b0.quo_rem(b1)
if r == 0:
return b1.monic()
a0 = b1
a1 = r
P.<x> = Zmod(n)[]
m1 = x^55537 - c1
m2 = pow(e_power, 65537, m1) - c2
print("starting gcd")
f = fast_polynomial_gcd(m1, m2)
print(long_to_bytes(int(-f(0))))
This finishes in about 6 minutes, much better than the 4.5 hours that it would have taken if one tried using the Euclidean algorithm.
Flag: grey{me0w_m3ow_s0lUtioN_t0o_Sl0w_4_m3-oW!!!}
Stirrer#
server.py
from subprocess import Popen, PIPE
from Crypto.Util.Padding import pad
from os import urandom
KEY = urandom(5)
key_int = int.from_bytes(KEY, byteorder='big')
def encrypt(pt):
pt = pad(pt, 5)
cproc = Popen(["./encrypt", str(len(pt)), str(key_int)], stdin=PIPE, stdout=PIPE)
out, err = cproc.communicate(pt)
return out
def main():
T = 0
while T < 1000:
try:
pt = input()
pt = bytes.fromhex(pt)
if (len(pt) > 10000):
print("Message too long.")
exit(1)
ct = encrypt(pt)
if pt == encrypt(KEY): # das crazy
print(open("flag.txt", "r").read())
exit(0)
print(ct.hex())
except Exception as e:
print("Error.")
exit(1)
T+=1
if __name__ == "__main__":
main()
encrypt.c
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <time.h>
#include <string.h>
#define N 5
uint8_t key[N];
// 8-bit left rotation
inline uint8_t rotl8(uint8_t x, int n) {
return (uint8_t)((x << n) | (x >> (8 - n)));
}
inline void block(uint8_t* state) {
for (int i = 0; i < N; i++)
state[i] = (state[i] + key[i]) & 0xFF;
state[0] = (state[0] + state[1]) & 0xFF;
state[3] ^= state[0];
state[3] = rotl8(state[3], 1);
state[2] = (state[2] + state[4]) & 0xFF;
state[0] ^= state[2];
state[0] = rotl8(state[0], 7);
state[1] = (state[1] + state[2]) & 0xFF;
state[4] ^= state[1];
state[4] = rotl8(state[4], 2);
for (int i = 0; i < N; i++)
state[i] = (state[i] + key[i]) & 0xFF;
}
void encrypt(uint8_t *pt, uint8_t *ct, size_t len) {
memcpy(ct, pt, len);
for (size_t i = 0; i < len; i+=5) {
for (int t = 0; t < 1000; t++) block(ct + i);
}
}
int main(int argc, char** argv) {
int LEN = atoi(argv[1]);
long KEY = atol(argv[2]);
key[0] = (KEY >> 32) & 0xff;
key[1] = (KEY >> 24) & 0xff;
key[2] = (KEY >> 16) & 0xff;
key[3] = (KEY >> 8) & 0xff;
key[4] = KEY & 0xff;
uint8_t *pt = malloc(LEN);
uint8_t *ct = malloc(LEN);
if (!pt || !ct) return 1;
fread(pt, sizeof *pt, LEN, stdin);
encrypt(pt, ct, LEN);
fwrite(ct, sizeof *ct, LEN, stdout);
free(pt);
free(ct);
return 0;
}
The challenge implements a custom block cipher operating on blocks of five bytes each, with a five byte key. We will first model one round of the encryption function in z3.
from z3 import *
k = [BitVec(f"k{i}", 8) for i in range(5)]
s = [BitVec(f"s{i}", 8) for i in range(5)]
def encrypt(s, k):
s = [i+j for i, j in zip(s, k)]
s[0] += s[1]
s[3] ^= s[0]
s[3] = RotateLeft(s[3], 1)
s[2] += s[4]
s[0] ^= s[2]
s[0] = RotateLeft(s[0], 7)
s[1] += s[2]
s[4] ^= s[1]
s[4] = RotateLeft(s[4], 1)
s = [i+j for i, j in zip(s, k)]
return s
print(encrypt(s, k))
# [
# RotateLeft(s0 + k0 + s1 + k1 ^ s2 + k2 + s4 + k4, 7) + k0,
# s1 + k1 + s2 + k2 + s4 + k4 + k1,
# s2 + k2 + s4 + k4 + k2,
# RotateLeft(s3 + k3 ^ s0 + k0 + s1 + k1, 1) + k3,
# RotateLeft(s4 + k4 ^ s1 + k1 + s2 + k2 + s4 + k4, 1) + k4
# ]
Let c be the ciphertext obtained from one round of encryption. It can be seen that c[1], c[2], and c[4] do not depend on s[0], s[3], k[0], or k[3]. We can then brute force for k[1], k[2], k[4] from a plaintext-ciphertext pair, then brute force the remaining two key bytes. This took about 40 seconds on my computer.
brute.c
// gcc brute.c -O3 -o brute
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <time.h>
#include <string.h>
#define N 5
uint8_t key[N];
// 8-bit left rotation
inline uint8_t rotl8(uint8_t x, int n) {
return (uint8_t)((x << n) | (x >> (8 - n)));
}
inline void block(uint8_t* state) {
for (int i = 0; i < N; i++)
state[i] = (state[i] + key[i]) & 0xFF;
state[0] = (state[0] + state[1]) & 0xFF;
state[3] ^= state[0];
state[3] = rotl8(state[3], 1);
state[2] = (state[2] + state[4]) & 0xFF;
state[0] ^= state[2];
state[0] = rotl8(state[0], 7);
state[1] = (state[1] + state[2]) & 0xFF;
state[4] ^= state[1];
state[4] = rotl8(state[4], 2);
for (int i = 0; i < N; i++)
state[i] = (state[i] + key[i]) & 0xFF;
}
void encrypt(uint8_t *pt, uint8_t *ct, size_t len) {
memcpy(ct, pt, len);
for (size_t i = 0; i < len; i+=5) {
for (int t = 0; t < 1000; t++) block(ct + i);
}
}
int main(int argc, char** argv) {
uint8_t pt[5] = {5, 5, 5, 5, 5};
uint8_t knownct[5] = {0x1a, 0x91, 0x1e, 0xd3, 0x8d};
uint8_t ct[5] = {0};
for (int b1 = 0; b1 < 256; ++b1) {
key[1] = b1;
for (int b2 = 0; b2 < 256; ++b2) {
key[2] = b2;
for (int b4 = 0; b4 < 256; ++b4) {
key[4] = b4;
encrypt(pt, ct, 5);
if (ct[1] == knownct[1] && ct[2] == knownct[2] && ct[4] == knownct[4]) {
// printf("possible: ??%02x%02x??%02x\n", b1, b2, b4);
for (int b0 = 0; b0 < 256; ++b0) {
for (int b3 = 0; b3 < 256; ++b3) {
key[0] = b0; key[3] = b3;
encrypt(pt, ct, 5);
if (ct[0] == knownct[0] && ct[3] == knownct[3]) {
printf("FOUND: %02x%02x%02x%02x%02x\n", b0, b1, b2, b3, b4);
}
}
}
}
}
}
}
return 0;
}
With the key obtained, we can then decrypt it with itself and submit it to the server to get the flag.
Flag: grey{obligatory_dont_roll_your_own_crypto_reference_i_hope_you_didnt_just_gpt_the_soln_else_ill_be_sad_:(}
Final thoughts#
Winning in ICO then bombing GreyCTF finals in such close succession was an experience. Even though both events were in person, I didn’t manage to meet many new people, and mostly interacted with ones that I knew, which was kind of sad. I also remember thinking to myself that I’ll retire from playing CTFs,7 but now that I’ve had some time to think about it, I don’t think I will; CTFs are too fun.
technically five; the first and last day were for arrival/departure ↩︎
some technical issues, and communication issues especially with the Singaporean team ↩︎
there were pwn and web challenges on the “defence” style day as well ↩︎
and didnt solve ↩︎
after talking with the challenge author i learnt that angr was the intended solution originally but it didnt work out; the flag still mentions angr ↩︎
i am thoroughly convinced that i cannot do well for in-person ctfs ↩︎
i say this after almost every ctf ↩︎